Question 1184018: Susan and Jenny run a 200 m race which Susan wins by 10 m. Jenny suggests that they run
another race, with Susan starting 10 m behind the starting line. Assuming they run at the same
speeds as in the first race, what is the outcome of the race?
Found 3 solutions by ikleyn, MathTherapy, greenestamps:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Susan and Jenny run a 200 m race which Susan wins by 10 m. Jenny suggests that they run
another race, with Susan starting 10 m behind the starting line. Assuming they run at the same
speeds as in the first race, what is the outcome of the race?
~~~~~~~~~~~~~~~~~~
Let x be the Susan's rate (in meters per second), and let y be the Jenny's rate.
Susan's time is  seconds; it is equal to seconds; it is equal to  , according to the condition.
So, we have , according to the condition.
So, we have  = =  , or , or  = =  = =  . (1)
Next, in the other scenario, Susan's time to complete 210 m run will be . (1)
Next, in the other scenario, Susan's time to complete 210 m run will be 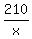 seconds,
while the Jenny's time to complete her run of 200 m will be seconds,
while the Jenny's time to complete her run of 200 m will be 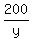 .
The problem asks which value is lesser, .
The problem asks which value is lesser, 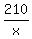 or or 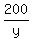 .
From (1), we have x = .
From (1), we have x =  , therefore
Susan's time will be , therefore
Susan's time will be 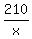 = =  = =  = =  = =  .
Obviously, it is less than the Jenny's time .
Obviously, it is less than the Jenny's time 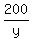 .
So, the conclusion is: Susan will win (will be first) in the second scenario run. ANSWER .
So, the conclusion is: Susan will win (will be first) in the second scenario run. ANSWER
Solved and thoroughly explained.
//////////////
There is even more easy and comprehensive explanation.
From the given part, Susan runs faster than Jenny.
They run 200 meters (Susan) and 190 meters (Jenny) in the same time.
If we add the same ANY arbitrary distance D (like 10 meters in the problem) to 200 m and 190 m respectively,
Susan will cover the new distance of 200 + D meters QUICKER than Jenny will cover her distance of 190 + D meters.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Susan and Jenny run a 200 m race which Susan wins by 10 m. Jenny suggests that they run
another race, with Susan starting 10 m behind the starting line. Assuming they run at the same
speeds as in the first race, what is the outcome of the race?
This TRAVEL problem, just like most of them involves using the travel formula: Distance = Speed * Time
Let Susan’s speed be S
Then time Susan took to complete the race = 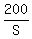 Then, Jenny’s speed, with her time also being
Then, Jenny’s speed, with her time also being 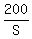 is is  If Susan starts 10 m behind the starting line, she’ll have to travel 200 + 10 = 210 m
Jenny, however, will travel 200 m
Time Susan takes to travel 210 m:
If Susan starts 10 m behind the starting line, she’ll have to travel 200 + 10 = 210 m
Jenny, however, will travel 200 m
Time Susan takes to travel 210 m: 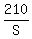 Time Jenny takes to travel 200 m:
Time Jenny takes to travel 200 m:  Susan’s time:
Susan’s time:  Comparing Susan’s time:
Comparing Susan’s time: 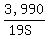 to Jenny’s time: to Jenny’s time: 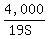 , we see that Susan’s time is less, so Susan will win the race, again! , we see that Susan’s time is less, so Susan will win the race, again!
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here is a very different approach to answering the question -- WITHOUT using distance = rate * time.
In the 200m race, Jenny completes 190m while Susan completes 200m. That means Jenny's speed is 19/20 of Susan's speed.
So Jenny and Susan will finish a race together if the distance Susan has to run is 20/19 of the distance Jenny has to run.
But in the second race, the distance Susan has to run is 210/200 = 21/20 of the distance Jenny has to run. And 21/20 (= 1 1/20) is less than 20/19 (= 1 1/19) -- so Susan will win this race also.
|
|
|