Question 1183278: I need help with this please. A baseball player throws a baseball from a height of 1 meter above the ground and its height is given by the equation 𝒉 = −𝟑. 𝟐𝒕^𝟐 + 𝟏𝟐.𝟖𝒕 + 𝟏, where 𝒉 is the height in metres above the ground, and t, in seconds, is its
time in the air [see the image below]. When, to the nearest tenth of a second, will the ball hit the ground? This is the image https://giannepaulaperalta.files.wordpress.com/2018/07/3075613-6448579381.jpg (you could pls copy and paste the link on a new tab). Also responding to the tutor that asked if I created this question on my own. To answer that no I didn't. This is a question from my assignments given to me by my teacher.
Answer by ikleyn(52937)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The basic formula for the height as the function of time is written INCORRECTLY in your post.
It has a FATAL ERROR, which makes the solution NONSENSICAL.
To get the basic knowledge on the subject, read my post to the end.
//////////////
The problems on a projectile thrown-shot-launched vertically up are very popular.
But, as I often observed, the students who meet such problems for the first time, often write
the basic equation incorrectly, because they do not understand the meaning of its terms.
Therefore, I wrote this introductory lesson specially for beginners who don't know the subject AT ALL.
If you have the formula for a height given to you as a function of time in the form
h(t) = -at^2 + bt + c, (1)
where "a", "b" and "c" are real numbers, a > 0, then in this formula
(a) the initial height is equal to the coefficient "c" value;
(b) the initial velocity is the coefficient "b" in the formula;
(c) the coefficient "a" value is half of the gravity acceleration.
For the Earth conditions, the gravity acceleration is g = 9.81 m/s^2,
if you use meters for height.
So, in this case, when you use meters as the measure of height, a =  = =  m/s^2 or 5 m/s^2 (approximate numerical value).
+--------------------------------------------------------------+
| It can not be 3.2 m/s^2, as it is written in your post. |
+--------------------------------------------------------------+
(d) To find the height at the time moment "t", simply substitute the value of "t" into the formula (1) and calculate.
(e) To find the time "t" when the height has a given value h = m/s^2 or 5 m/s^2 (approximate numerical value).
+--------------------------------------------------------------+
| It can not be 3.2 m/s^2, as it is written in your post. |
+--------------------------------------------------------------+
(d) To find the height at the time moment "t", simply substitute the value of "t" into the formula (1) and calculate.
(e) To find the time "t" when the height has a given value h =  , substitute h = , substitute h =  into equation (1)
and solve equation
h(t) = -at^2 + bt + c = into equation (1)
and solve equation
h(t) = -at^2 + bt + c =  . (2)
(f) To find the time when the height is maximal, use the formula . (2)
(f) To find the time when the height is maximal, use the formula
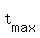 = = 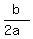 . (3)
(g) To find the maximal height, substitute the time value t= . (3)
(g) To find the maximal height, substitute the time value t= 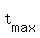 of the formula (3) into the formula (1). of the formula (3) into the formula (1).
What's all you need to know.
To see numerous examples of solved problems, look into the lessons
- Problem on a projectile moving vertically up and down
- Problem on an arrow shot vertically upward
- Problem on a ball thrown vertically up from the top of a tower
- Problem on a toy rocket launched vertically up from a tall platform
- OVERVIEW of lessons on a projectile thrown/shot/launched vertically up
in this site.
----------------
If this introduction is helpful to you, I will be happy.
If it will be not enough to you to solve the problem, come again,
but with one indispensable condition: your equation MUST be written correctly.
/\/\/\/\/\/\/\/
Regarding your teacher, you may show him (or her) this my post. Or, if you hesitate do it,
give me his (or her) contact, and I will ask him (or her), why he (or she) gives wrong assignments.
In the country where I growth and got my school and university education,
it was UNTHINKABLE that a Math teacher gave an incorrect assignment.
I can not recall even one single such case.
It was not because the teachers were absolutely perfect - they were normal people (very professional, although).
But the educational system itself was so perfect that failed cases were impossible to happen inside of this system.
|
|
|