Question 1183238: Hayden is playing with a toy airplane. The height of the airplane, in metres, is given by the relation
h = −5t^2+ 18t + 1, where t is the number of seconds since the plane was launched. At time t, the
horizontal distance travelled by the airplane is given by d = 4. 5t.
a) For how long will the airplane be in the air, rounded to the nearest tenth of a second?
b) How far will the airplane travel horizontally by the time it hits the ground, rounded to the
nearest tenth of a
metre?
c) At what time(s), rounded to the nearest tenth of a second, will the airplane reach a height of
12 m?
d) What is the maximum height or the plane?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Hayden is playing with a toy airplane. The height of the airplane, in metres, is given by the relation
h = −5t^2+ 18t + 1, where t is the number of seconds since the plane was launched. At time t, the
horizontal distance travelled by the airplane is given by d = 4.5t.
a) For how long will the airplane be in the air, rounded to the nearest tenth of a second?
b) How far will the airplane travel horizontally by the time it hits the ground, rounded to the nearest tenth of a metre?
c) At what time(s), rounded to the nearest tenth of a second, will the airplane reach a height of 12 m?
d) What is the maximum height or the plane?
~~~~~~~~~~~~~~
From the equations, the initial vertical speed is 18 m/s up; the initial height is 1 meter (at the start);
horizontal speed is 4.5 m/s, the constant value during the flight.
a) For how long will the airplane be in the air, rounded to the nearest tenth of a second?
The toy airplane is in the air until h(t) > 0. The airplane get the ground when h(t) = 0.
THEREFORE, to find the time the airplane is in the air, we should solve this quadratic equation
-5t^2 + 18t + 1 = 0
 = = 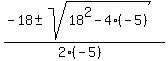 = =  .
Of the two roots, we chose the positive one, which is t = .
Of the two roots, we chose the positive one, which is t = 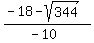 = 3.7 seconds (rounded as requested).
So, question (a) is answered: the airplane is in the air 3.7 seconds. = 3.7 seconds (rounded as requested).
So, question (a) is answered: the airplane is in the air 3.7 seconds.
b) How far will the airplane travel horizontally by the time it hits the ground, rounded to the nearest tenth of a metre?
Simply multiply the horizontal component of the speed by the time
horizontal distance = 4.5 * 3.7 = 16.45 meters. ANSWER
c) At what time(s), rounded to the nearest tenth of a second, will the airplane reach a height of 12 m?
To answer, we should solve this quadratic equation
-5t^2 + 18t + 1 = 12
-5t^2 + 18t - 11 = 0
 = = 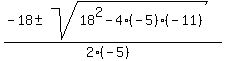 = =  . .
 = =  = 0.78 s; = 0.78 s;  = = 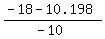 = 2.82 s.
The smaller value of t is the ascending flight; the larger value of t is the descending flight.
Part (c) is completed. = 2.82 s.
The smaller value of t is the ascending flight; the larger value of t is the descending flight.
Part (c) is completed.
d) What is the maximum height or the plane?
The highest point of the flight is the vertex of the quadratic function h(t).
The value of "t" is t = "  " = " =  = = 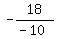 = 1.8.
It means that the airplane reaches the maximum height at t= 1.8 seconds.
The maximum height is the value of the height function at t= 1.8 = 1.8.
It means that the airplane reaches the maximum height at t= 1.8 seconds.
The maximum height is the value of the height function at t= 1.8
 = =  = 17.2 meters. ANSWER = 17.2 meters. ANSWER
The problem is just solved. // All questions are answered.
==================
To see many other solved similar and different problems, see the lessons
- Introductory lesson on a projectile thrown-shot-launched vertically up
- Problem on a projectile moving vertically up and down
- Problem on an arrow shot vertically upward
- Problem on a ball thrown vertically up from the top of a tower
- Problem on a toy rocket launched vertically up from a tall platform
- Problem on a projectile thrown horizontally
- Problems on projectile launched at an angle to horizon
Consider these lessons as your textbook, handbook, tutorials and (free of charge) home teacher.
Read them attentively and learn how to solve this type of problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Projectiles launched/thrown and moving vertically up and dawn".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|