SOLUTION: The sum of the first ten terms of an arithmetic progression consisting of positive integer terms is equal to the sum of the 20th, 21st and 22nd term. If the first term is less than

Algebra ->  Finance -> SOLUTION: The sum of the first ten terms of an arithmetic progression consisting of positive integer terms is equal to the sum of the 20th, 21st and 22nd term. If the first term is less than      Log On


   

Question 1182882: The sum of the first ten terms of an arithmetic progression consisting of positive integer terms is equal to the sum of the 20th, 21st and 22nd term. If the first term is less than 20, find how many terms are required to give a sum of 960.
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


The sum of the first n terms of an arithmetic progression with first term a and constant difference d is

S%28n%29=%28n%282a%2B%28n-1%29d%29%29%2F2

We will use that formula twice in solving this problem.

The sum of the first ten terms is

S%2810%29+=+%2810%282a%2B9d%29%29%2F2

The sum of the 20th, 21st, and 22nd terms is three times the 21st term:

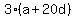
3%28a%2B20d%29

The problem then tells us

%2810%282a%2B9d%29%2F2%29=3%28a%2B20d%29
10a%2B45d=3a%2B60d
7a=15d

The sequence contains only positive integers; and the first term a is less than 20. Since 7 and 15 have no common factor, the only solution that meets the requirements is a=15 and d=7. So the progression is

15, 22, 29, 36, ...

The problem says to find the number of terms n for which the sum is 960:

S%28n%29+=+%28n%2830%2B%28n-1%297%29%29%2F2+=+960

30n%2B7n%5E2-7n+=+1920
7n%5E2%2B23n-1920+=+0

Since that won't factor easily, use the quadratic formula to find n=15.

ANSWER: 15 terms of the sequence will have a sum of 960.

CHECK:
1st term 15
10th term 15+9(7)=78
21st term 15+20(7)=155

sum of first 10 terms: %2810%2815%2B78%29%29%2F2=5%2893%29=465
sum of 20th, 21st, and 22nd terms: 3%28155%29=465