Question 1182879: Find all numbers between 200 and 500 which have exactly 9 factors.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find all numbers between 200 and 500 which have exactly 9 factors.
~~~~~~~~~~~~~~~~~~
Notice that 9 =  , and it tells us that the south number N is the square
of the integer positive number " n ", which is the product of two prime numbers.
So, we look into the open interval from , and it tells us that the south number N is the square
of the integer positive number " n ", which is the product of two prime numbers.
So, we look into the open interval from 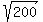 ~ 14.1 to ~ 14.1 to 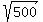 ~ 22.4
and search there the numbers " n " that are the products of two different prime numbers.
We find there ONLY THREE such numbers 15, 21 and 22, so the ANSWER to the problem's question
are the numbers ~ 22.4
and search there the numbers " n " that are the products of two different prime numbers.
We find there ONLY THREE such numbers 15, 21 and 22, so the ANSWER to the problem's question
are the numbers 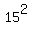 = 225, = 225, 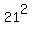 = 441. and = 441. and 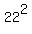 = 484. = 484.
Solved.
--------------
About the relevant theorem from the number theory on the number of divisors to any integer positive number see the lesson
- Problems on divisors of a given number
in this site.
This theorem states
For integer number N = 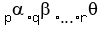 , where p, q, . . . , r are prime divisors
and , where p, q, . . . , r are prime divisors
and  , ,  , . . . , , . . . ,  are integer exponents (indexes), the number of divisors is are integer exponents (indexes), the number of divisors is  . .
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I will assume, since you are working a problem like this, that you know how to find the number of factors of a given number.
To get exactly 9 factors, the number can be either
(a) 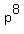 -- the 8th power of a single prime p, because 8+1=9; or -- the 8th power of a single prime p, because 8+1=9; or
(b) 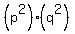 -- the product of the squares of two primes p and q, because (2+1)(2+1)=9 -- the product of the squares of two primes p and q, because (2+1)(2+1)=9
For case (a), 2^8=256, which is in the required range.
For case (b), we need the number to be the product of two primes; and the number must be between sqrt(200) and sqrt(500) -- or 15 to 22, inclusive. The numbers that satisfy those conditions are 15=3*5, 21=3*7, and 22=2*11.
ANSWER:
256 = 2^8
225 = 15^2
441 = 21^2
484 = 22^2
|
|
|