Question 1182800: How many pairs (a,b) of positive integers are there such that a and b are factors of 6^6 and a is a factor of b?
Found 3 solutions by ikleyn, greenestamps, robertb:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many pairs (a,b) of positive integers are there such that "a" and "b" are factors of 6^6 and "a" is a factor of "b" ?
~~~~~~~~~~~~~~~~~
In this problem, the terms (the words) "factor", "factors" are used as synonyms of the term "divisor",
as it is clear from the context.
It means that when the problem says "a" and "b" are factors of  , it DOES NOT necessary mean that a*b = , it DOES NOT necessary mean that a*b =  . .
According to the context, it ONLY MEANS that "a" and "b" are the DIVISORS of  . .
It is how I read, understand, interpret and solve this problem.
First of all,  = =  = = 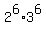 .
So, the divisors of the number .
So, the divisors of the number  = = 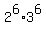 are all those and only those integer positive numbers are all those and only those integer positive numbers 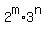 ,
where 0 <= m <= 6, 0 <= n <= 6.
From this notice, it becomes clear that the total number of divisors " b " to the number ,
where 0 <= m <= 6, 0 <= n <= 6.
From this notice, it becomes clear that the total number of divisors " b " to the number  is 7*7 = 49.
+---------------------------------------------------------------------------+
| So, we solved part of the problem, but not the whole problem, yet. |
| Now I will analyse the remaining part. |
+---------------------------------------------------------------------------+
For any factor "a" of b = is 7*7 = 49.
+---------------------------------------------------------------------------+
| So, we solved part of the problem, but not the whole problem, yet. |
| Now I will analyse the remaining part. |
+---------------------------------------------------------------------------+
For any factor "a" of b = 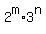 , the "a" has the form a = , the "a" has the form a = 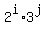 , where 0 <= i <= m, 0 <= j <= n.
It implies that for any of 49 factors b = , where 0 <= i <= m, 0 <= j <= n.
It implies that for any of 49 factors b = 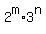 , there are (m+1)*(n+1) factors "a" to "b".
Hence, when we calculate the number of pairs (a,b), as described in the problem, we sum up all these products (m+1)*(n+1)
for all pairs (m,n) with m and n from 0 to 6 inclusive.
From this point, it is not difficult to get the idea that our sough number of pairs (a,b) is THIS PRODUCT
(1 + 2 + 3 + . . . + 6 + 7)*(1 + 2 + 3 + . . . + 6 + 7).
Each factor in parentheses is the sum of the first 7 natural numbers S = , there are (m+1)*(n+1) factors "a" to "b".
Hence, when we calculate the number of pairs (a,b), as described in the problem, we sum up all these products (m+1)*(n+1)
for all pairs (m,n) with m and n from 0 to 6 inclusive.
From this point, it is not difficult to get the idea that our sough number of pairs (a,b) is THIS PRODUCT
(1 + 2 + 3 + . . . + 6 + 7)*(1 + 2 + 3 + . . . + 6 + 7).
Each factor in parentheses is the sum of the first 7 natural numbers S = 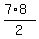 = 7*4 = 28.
Therefore, the answer to the problem's question is "there are 28*28 = 784 such pairs (a,b)".
ANSWER. There are 784 such pairs (a,b). = 7*4 = 28.
Therefore, the answer to the problem's question is "there are 28*28 = 784 such pairs (a,b)".
ANSWER. There are 784 such pairs (a,b).
Solved.
/////////////
In my solution, I treat the notion/conception of a divisor to a number N
as any proper divisor AND/OR improper divisors as the number of " 1 " and the number N itself.
Such treatment makes the solution easier; from the other hand side, it is not prohibited
by the text or the context to treat it this way.
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! I will have to go with ikleyn's solution here.
The problem with greenestamps' solution is that he essentially assumes that a*b = 6^6, which is an incorrect assumption.
ikleyn's solution is correct, but the solution requires a bit of motivation combinatorially, especially when explaining
(1+2+3+4+5+6+7)*(1+2+3+4+5+6+7) = 28^2 = 784.
In fact the problem can be generalized further to the number A^n*B^m and not only to 2^6*3^6.
(So the bases 2 and 3 are irrelevant, and A and B can be any distinct positive integers both greater than 1.)
In this case the number of ordered pairs will be ((n+1)(n+2))/2*((m+1)(m+2))/2 = (n+1)(n+2)(m+1)(m+2)/4.
|
|
|