Question 1182753: A six-sided dice has the numbers 1,2,2,3,3 and 3 on its faces. Two such dice are rolled and a score is made by adding the numbers on the uppermost faces. The probability of rolling an odd score is?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Start preparing the quadratic table with the horizontal and vertical input
1 2 2 3 3 3
1
2
2
3
3
3
The values in the cells of this table are "scores", that are the sums of the
"horizontal" and "vertical" input values.
You should to find out the number of ODD values in the 36 cells of the table.
+--------------------------------------------------------------+
| But do not hurry to fill this table, adding the numbers. |
| We will solve the problem by another way. |
+--------------------------------------------------------------+
Part of odd values of the table are the sums of the vertical odd and horizontal even input values,
and there are (1+3)*2 = 4*2 = 8 such cells in the table.
Another part of odd values of the table are the sums of the vertical even and horizontal odd input values,
and there are 2*(1+3) = 2*4 = 8 such cells in the table.
Also, it is clear / (obvious) that Part 1 and Part 2 cells are different (these sets are DISJOINT).
Thus, in all, there are 8+8 = 16 odd sums in the table,
giving the ANSWER for the probability P = 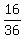 = =  . .
Solved.
//////////////
Notice that the (hidden) meaning of this problem is to give the answer WITHOUT making this stupid job
ADDING the numbers in the cells, and I managed to solve the problem in this way, explaining it to you.
Do not forget to post your "THANKS" to me for my teaching.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
To get an odd score, there must be either an odd number on die A and an even number on die B, or an even number on die A and an odd number on die B:
P(odd sum) = 
ANSWER: 4/9
|
|
|