Question 1182420: How long will it take $3,000 to grow to $14,000 if it is invested at 5% compounded monthly?
How many years?
Found 4 solutions by mananth, ikleyn, CPhill, n2:
Answer by mananth(16949)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Find number of years
Principal P = 3000
Amount= 14000
years=n
compounded (t) 12
Rate = 5 0.004166667
Amount = P*((n+r)/n)^n
14000 = 3000 *( 1 + 0.004166667 )^ n*t
4.666666667 = *( 1 + 0.004166667 )^ n* 12
log 4.666666667 = 12 n *log 1.004166667
1.540445041 = 12 0.00415801 *n
30.87 = n
30.87 years
Answer by ikleyn(53570)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How long will it take $3,000 to grow to $14,000 if it is invested at 5% compounded monthly?
How many years?
~~~~~~~~~~~~~~~~~~~~~~~~~
In the post by @mananth, the answer is incorrect.
In this problem, same as many other similar problems,
the answer should be expressed in integer number of compounding periods.
Principal P = 3000
Amount= 14000
number of compounding = n
compounded 12 times per year
Nominal rate per year = 5%
Effective rate per month r = 0.05/12
Future value = 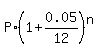 14000 =
14000 = 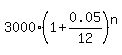 4.666666667 =
4.666666667 = 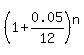 log(4.666666667) =
log(4.666666667) = 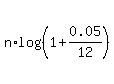 n =
n = 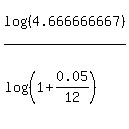 = 370.4764986 (approx.)
This decimal number, 370.4764986, should be rounded up to the closest integer number 371
in order for the bank would be in position to make the last compounding.
ANSWER. The value at the account first time will exceed $14000 after 371 month, or 30 years and 11 months. = 370.4764986 (approx.)
This decimal number, 370.4764986, should be rounded up to the closest integer number 371
in order for the bank would be in position to make the last compounding.
ANSWER. The value at the account first time will exceed $14000 after 371 month, or 30 years and 11 months.
Solved correctly, properly and accurately.
--------------------------
When solving such problems on discrete compounding, always remember that the future value
is NOT a continuous function of time. In opposite, it is piecewise constant function,
which changes its values at the end of each compounding period, ONLY.
Answer by CPhill(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find number of years
Principal P = 3000
Amount= 14000
years=n
compounded (t) 12
Rate = 5 0.004166667
Amount = P*((n+r)/n)^n
14000 = 3000 *( 1 + 0.004166667 )^ n*t
4.666666667 = *( 1 + 0.004166667 )^ n* 12
log 4.666666667 = 12 n *log 1.004166667
1.540445041 = 12 0.00415801 *n
30.87 = n
30.87 years
Answer by n2(43)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How long will it take $3,000 to grow to $14,000 if it is invested at 5% compounded monthly?
How many years?
~~~~~~~~~~~~~~~~~~~~~~~~~
In the post by @CPhill, the answer is incorrect.
In this problem, same as many other similar problems,
the answer should be expressed in integer number of compounding periods.
Principal P = 3000
Amount= 14000
number of compounding = n
compounded 12 times per year
Nominal rate per year = 5%
Effective rate per month r = 0.05/12
Future value = 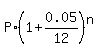 14000 =
14000 = 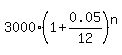 4.666666667 =
4.666666667 = 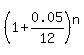 log(4.666666667) =
log(4.666666667) = 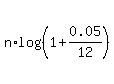 n =
n = 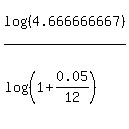 = 370.4764986 (approx.)
This decimal number, 370.4764986, should be rounded up to the closest integer number 371
in order for the bank would be in position to make the last compounding.
ANSWER. The value at the account first time will exceed $14000 after 371 month, or 30 years and 11 months. = 370.4764986 (approx.)
This decimal number, 370.4764986, should be rounded up to the closest integer number 371
in order for the bank would be in position to make the last compounding.
ANSWER. The value at the account first time will exceed $14000 after 371 month, or 30 years and 11 months.
Solved correctly, properly and accurately.
--------------------------
When solving such problems on discrete compounding, always remember that the future value
is NOT a continuous function of time. In opposite, it is piecewise constant function,
which changes its values at the end of each compounding period, ONLY.
|
|
|