Question 1181745: Suppose you have $2500 in your savings account at the end of a certain period of time. You invested $1700 at 6.75% simple annual interest rate. How long in years was your money invested? (State your result to the nearest hundredth of a year.)
Found 4 solutions by Solver92311, ikleyn, MathTherapy, greenestamps:
Answer by Solver92311(821)   (Show Source):
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
John misread the problem.
I came to bring a correct solution.
We have simple interest rate, so our equation is
2500 = 1700*(1 + 0.0675*t).
From the equation,
t = 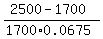 = 6.972 years = 7 years (rounded). ANSWER
Solved.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
Suppose you have $2500 in your savings account at the end of a certain period of time. You invested $1700 at 6.75% simple annual interest rate. How long in years was your money invested? (State your result to the nearest hundredth of a year.)
SI accumulated/Future Value formula: A = P(1 + TR)
2,500 = 1,700(1 + .0675T) ------ Substituting 2,500 for A, 1,700 for P, and .0675 (6.75%) for R
Time, or 
Your answer though should be rounded to the NEXT whole number, or to 7, making it 7 FULL YEARS, since interest rate is ANNUAL.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
In case you were confused by the different response you have received....
Tutor @Solver92311 misread the problem as being compound interest instead of simple interest.
Tutor @ikleyn "came to bring the right answer" and showed the correct calculations; but somewhere her actual calculations went wrong.
Tutor @MathTherapy used the right calculation and shows the right answer.
|
|
|
