Question 1181093: A theater has tickets at $6 for adults, $3 for students and $2 for children under 12 years old. A total of 280 tickets were sold for one showing with total revenue of $910. If the number of adult tickets plus the number of student tickets was equal to the number of child tickets, then how many of each type of ticket were sold for the showing?
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
A theater has tickets at $6 for adults, $3 for students and $2 for children under 12 years old.
A total of 280 tickets were sold for one showing with total revenue of $910.
If the number of adult tickets plus the number of student tickets was equal to the number of child tickets,
then how many of each type of ticket were sold for the showing?
~~~~~~~~~~~~~~~~~~
From the condition, an attentive reader sees momentarily, that the number of child tickets is HALF of 280 tickets,
i.e. 140 tickets, and that the combined number of adult tickets and student tickets is another half of 280 tickets, i.e. 140 tickets.
THEREFORE, for combined adult tickets and student tickets we have THIS INFO:
+-----------------------------------------------------------------------------------+
| their total combined number is 140 and their cost is 910 - 2*140 = 630 dollars. |
+-----------------------------------------------------------------------------------+
So, now you have the problem for two unknowns, ONLY, or, if you want, for one single unknown, which is EASIER TO SOLVE (!)
Let x be the number of adult tickets; then the number of student tickets is 140-x, and you can writhe this MONEY equation
6x + 3(140-x) = 630 dollars.
From this equation
x = 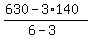 = 70.
ANSWER. 70 adult tickets; 140-70 = 70 student tickets and 140 child tickets.
Solved.
-----------------
From my solution, learn HOW I reduced the problem to one single equation in one unknown.
It is the major lesson to learn from my post.
|
|
|
