Question 1180216: Which hyperbolas have one vertex in common with the hyperbola
(y-4)^2/7^2-(x+6)^2/8^2=1?
a. (y-8)^2/5^2-(x+6)^2/6^2=1
b. (x-1)^2/8^2-(y-11)^2/7^2=1
c. (x+15)^2/9^2-(y+3)^2/5^2=1
d. (y-6)^2/6^2-(x+6)^2/4^2=1
e. (y-23)^2/12^2-(x+6)^2/8^2=1
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Which hyperbolas have one vertex in common with the hyperbola

Up-down hyperbola with center ( , ,  )= ( )= ( , ,  ), ),  , , 
The vertices:
( , , 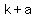 ), ( ), ( , , 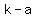 ) )
=>( , , 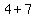 ), ( ), ( , , 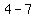 ) )
=>( , ,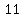 ), ( ), ( , ,  ) )
a.

center ( , ,  )= ( )= ( , ,  ), ),  , , 
The vertices:
( , , 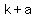 ), ( ), ( , , 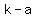 ) )
=>( , , 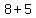 ), ( ), ( , , 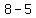 ) )
=>( , ,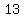 ), ( ), ( , ,  ) )
b.

Right-left hyperbola with ( , , )= ( )= ( , ,  ), ),  , , 
The vertices
(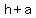 , ,  ), ( ), (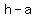 , , ) )
=>(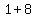 , ,  ), ( ), (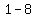 , ,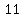 ) )
=>( , ,  ), ( ), ( , ,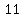 ) )
c.

Right-left hyperbola with ( , , )= ( )= ( , ,  ), ),  , , 
The vertices
(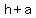 , ,  ), ( ), (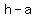 , , ) )
=>(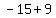 , ,  ), ( ), (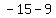 , , ) )
=>( , ,  ), ( ), ( , , ) )
d.

Up-down hyperbola with center ( , ,  )= ( )= ( , ,  ), ),  , , 
The vertices:
( , , 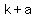 ), ( ), ( , , 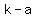 ) )
=>( , , 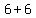 ), ( ), ( , , 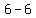 ) )
=>( , , ), ( ), ( , ,  ) )
e.

Up-down hyperbola with center ( , ,  )= ( )= ( , , 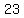 ), ),  , , 
The vertices:
( , , 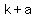 ), ( ), ( , , 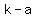 ) )
=>( , , 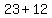 ), ( ), ( , , 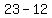 ) )
=>( , , ), ( ), ( , ,  ) )
hyperbolas which have one vertex in common with the given hyperbola:
c has =>( , ,  ) )
e has =>( , ,  ) )
|
|
|