Question 1179691: The area of the region under the curve of the function f(x) = 5x + 7 on the interval [1, b] is 88 square units, where b > 1.
the value of b is ?
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
This problem can be solved easily without calculus. The given function is a straight line, so the area under the curve on the interval [1,b] is a trapezoid. The area of a trapezoid is
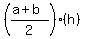
where h is the height and a and b are the lengths of the two bases.
For this problem, the height is (b-1); the two bases are f(1)=12 and f(b)=5b+7.




Note this is the same equation the other tutor ends up with using calculus.
She then goes on, as she always does, to magically separate the middle term 14b into two parts, producing a quadratic with four terms that can be factored by grouping. That's fine for showing the solution -- but it does nothing to teach the student how the factoring is done.
So let me take a bit of time here to talk about ways to factor a quadratic like this. There are many methods that are taught; most of them that I have seen consist of well defined steps that mysteriously lead to the right factorization.
I prefer one that calls on the student to use his powers of reasoning to obtain the answer.
In this case we want a factorization of the form

Since the b^2 term comes from (pb)(rb), and the coefficient of b^2 in the quadratic is 5, clearly p and r have to be 5 and 1, in some order. We can assume p=5 and r=1, giving us

Now look at the constant term in the quadratic: -195. That constant comes from q times s: 
We can see that q and s are of opposite sign; and we can see that one of them contains 5 as a factor.
Here is the where the logical reasoning makes what looks like a big problem much easier. If q contained a factor of 5, then the two terms in the binomial (pb+q) would have a common factor of 5. That would make the quadratic have a common factor of 5; but it does not. So q cannot contain a factor of 5; so s must contain a factor of 5.
-195 is 5(-39); at this point we can play with the signs of the two binomial factors and the possible values of q and s to find the combination that gives us the correct middle term.
With a little playing around like that, we find

That gives us possible values of -39/5 or 5 for b; the statement of the problem asking us to find the area under the curve on the interval [1,b] means we choose the positive value for b.
So b=5, and now we have all we need to find the area as the area of a trapezoid; its height is b-1=4; the bases are f(1)=12 and f(5)=32; the area is

|
|
|