Question 1179373: Use a determinant to find an equation of the line passing through the points
(x, y).
(−2, 5), (4, 1)
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52786)   (Show Source):
You can put this solution on YOUR website! .
It can be done in different ways.
I will show and explain one of them to you, the most simplest,
which you can, probably, will remember and understand all your life.
You have two vectors with components
(4-(-2), 1 - 5) = (6,-4) (starts at (-2,5), ends at (4,1) )
and
(x-4,y-1) (starts at (4,1); ends at (x,y) )
You want these two vectors be parallel (or antiparallel, does not matter).
It means that the determinant, composed of the components of these vectors is equal to zero
det 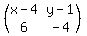 = 0. ANSWER
It is your equation, same as
-4*(x-4) - 6*(y-1) = 0. (*) ANSWER
You can simplify the resulting equation (*) any way as you want.
Solved, explained and completed.
Answer by MathLover1(20850)  (Show Source):
|
|
|
