Question 1177086: A consumer goods company recruits several graduating students from universities each year. Concerned about the high cost of training new employees, the company instituted a review of attrition among new recruits. Over five years, 30% of new recruits came from a local university, and the balance came from a more distant universities. Of the new recruits, 20% of those who were students from a local university resigned within two years, while 45% of other students resigned. Given that a student resigned within two years, what is the probability that she hired from
a) a local university?
b) a more distant university?
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely, let's break down this problem using Bayes' Theorem.
**Understanding the Problem**
* **Events:**
* L: Recruited from a local university.
* D: Recruited from a distant university.
* R: Resigned within two years.
* **Given Probabilities:**
* P(L) = 0.30 (30% from local)
* P(D) = 0.70 (70% from distant)
* P(R|L) = 0.20 (20% of local resigned)
* P(R|D) = 0.45 (45% of distant resigned)
**What We Need to Find**
* a) P(L|R): Probability of being from a local university given resignation.
* b) P(D|R): Probability of being from a distant university given resignation.
**Applying Bayes' Theorem**
Bayes' Theorem states: P(A|B) = [P(B|A) * P(A)] / P(B)
In our case:
* P(L|R) = [P(R|L) * P(L)] / P(R)
* P(D|R) = [P(R|D) * P(D)] / P(R)
**Calculating P(R) (Total Probability of Resignation)**
We need to find the overall probability of resignation, P(R). We can do this using the law of total probability:
* P(R) = P(R|L) * P(L) + P(R|D) * P(D)
* P(R) = (0.20 * 0.30) + (0.45 * 0.70)
* P(R) = 0.06 + 0.315
* P(R) = 0.375
**Solving for a) P(L|R)**
* P(L|R) = [P(R|L) * P(L)] / P(R)
* P(L|R) = (0.20 * 0.30) / 0.375
* P(L|R) = 0.06 / 0.375
* P(L|R) = 0.16
**Solving for b) P(D|R)**
* P(D|R) = [P(R|D) * P(D)] / P(R)
* P(D|R) = (0.45 * 0.70) / 0.375
* P(D|R) = 0.315 / 0.375
* P(D|R) = 0.84
**Answers**
* a) The probability that a student who resigned within two years was hired from a local university is 0.16 or 16%.
* b) The probability that a student who resigned within two years was hired from a distant university is 0.84 or 84%.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A consumer goods company recruits several graduating students from universities each year.
Concerned about the high cost of training new employees, the company instituted a review
of attrition among new recruits. Over five years, 30% of new recruits came from a local
university, and the balance came from a more distant universities. Of the new recruits,
20% of those who were students from a local university resigned within two years,
while 45% of other students resigned. Given that a student resigned within two years,
what is the probability that she hired from
a) a local university?
b) a more distant university?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Below is a simple and straightforward solution.
Let X be the total number of students under consideration.
Of them, 0.3*X are from local university; 0.7*X are from distant universities.
The number of students from local university, who were resigned, is 0.2*0.3*X.
The number of students from distant universities, who were resigned, is 0.45*0.7*X.
The total number of students, who were resigned, is (0.2*0.3*X + 0.45*0.7*X).
Question (a) asks about the ratio 0.2*0.3*X to this sum (0.2*0.3*X + 0.45*0.7*X).
So, ANSWER to question (a) is
P(A) = 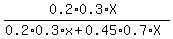 = cancel X and calculate =
= = cancel X and calculate =
= 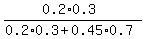 = 0.16.
Question (b) asks about the ratio 0.45*0.7*X to the sum (0.2*0.3*X + 0.45*0.7*X).
So, ANSWER to question (b) is
P(b) = = 0.16.
Question (b) asks about the ratio 0.45*0.7*X to the sum (0.2*0.3*X + 0.45*0.7*X).
So, ANSWER to question (b) is
P(b) =  = cancel X and calculate =
= = cancel X and calculate =
= 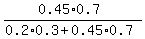 = 0.84.
Notice that the sum 0.16 + 0.84 is equal to 1, or 100%, which confirms our calculations. = 0.84.
Notice that the sum 0.16 + 0.84 is equal to 1, or 100%, which confirms our calculations.
Solved.
---------------------
Post-solution notice
Notice that my solution is simpler than what by @CPhill, and it does not refer to other theorems:
it is STRAIGHTFORWARD.
If a student solves the problem by the method, shown in the post by @CPhill, it means and it clearly 
that the student solves the problem by touch, following and repeating the recipes from others
like a woodpecker and without his or her own understanding.
If a student solves the problem by the method from this my post, it means and it clearly 
that the student understands everything from scratch to the end, and is able to think on his or her own.
Actually, a good level student should write these calculation formulas in one breath,
based on his or her own common sense. It is a sign and a signal of full understanding,
it is a sign of achieving a good level, and it is what I want to teach you.
|
|
|