Question 1177067: A pension fund manager decides to invest a total of at most $40 million in U.S. Treasury bonds paying 3% annual interest and in mutual funds paying 5%
annual interest. He plans to invest at least $5 million in bonds and at least $20 million in mutual funds. Bonds have an initial fee of $100 per million dollars, while the fee for mutual funds is $200 per million. The fund manager is allowed to spend no more than $7000 on fees. How much should be invested in each to maximize annual interest? What is the maximum annual interest?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let x = the amount invested in bonds.
let y the amount invested in mutual funds.
everything will be converted to millions for ease of presentation.
your constraint functions are:
x + y <= 40
x >= 5
y >= 20
.0001 * x + .0002 * y <= .007
x >= 0
y >= 0
your objective function is
.03 * x + .05 * y
this is what you want to maximize.
using the desmos.com calculator, you would graph the opposite of these constraint functions.
the coordinate points on the area of the graph that is not shaded, and the coordinate points on the lines themselves, if the inequalities are expressed as <= or >=, will be in the feasible region.
if the inequalities are expressed as < or >, then the coordinate points on the lines themselves are not included in the feasible region.
the graph looks like this.
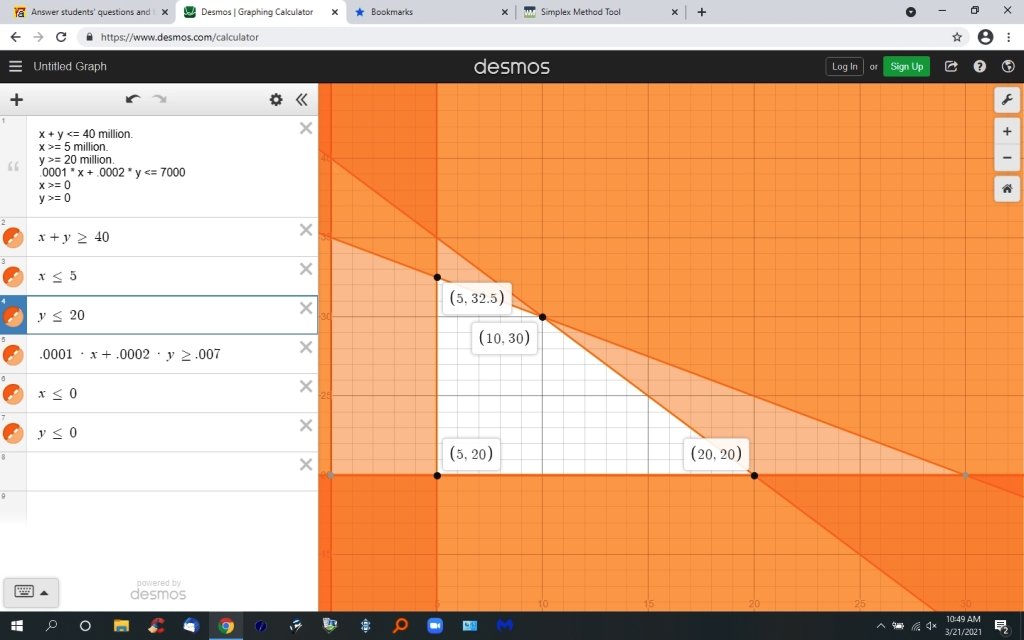
you would evaluate the objective function at each of the corner points of the feasible region on the graph.
the coordinate points that contain the maximum value for the objective function is your maximum solution.
i created a chart that showed the following:
a b c d
(5,32.5) 1.775 37.5 .007
(10,30) 1.8 40 .007
(5,20) 1.15 25 .0045
(20,20) 1.6 40 .006
column a is the coordinate points in (x,y) format.
x represents the amount invested in bonds.
y represents the amount invested in mutual funds.
column b = .03 * x + .05 * y
this is the profit.
column c = x + y
this is the total amount invested.
column d = .0001 * x + .0002 * y
this is the total amount paid out in fees.
from the table, it's clear that all of the constraints have been met for all of the options at the corner point of the feasible region.
the coordinate points with the maxim profit are at (x,y) = (10,30).
this means 10 million invested in bonds and 30 million invested in mutual funds.
you can see that the profit is 1.8 million with 40 million invested and 7000 paid out in fees (.007 million is equal to 7000).
the maximum interest is 1.8 million with 10 million invested in bonds and 30 million invested in mutual funds.
|
|
|