Question 1176067: A state lotto has a prize that pays $1,700 each week for 40 years.
Find the total value of the prize: $
Correct
If the state can earn 3% interest on investments, how much money will they need to put into an account now to cover the weekly prize payments?
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely! Let's calculate the total value of the prize and the amount needed to cover the weekly payments.
**1. Total Value of the Prize**
* Weekly prize: $1,700
* Years: 40
* Weeks per year: 52
Total value = Weekly prize * Weeks per year * Years
Total value = $1,700 * 52 * 40
Total value = $3,536,000
**2. Present Value Calculation**
To determine how much money the state needs to invest now, we need to calculate the present value of the annuity.
* Weekly payment: $1,700
* Interest rate: 3% per year
* Years: 40
Since the payments are weekly, we need to adjust the interest rate to a weekly rate.
* Annual interest rate: 0.03
* Weekly interest rate: 0.03 / 52 ≈ 0.000576923
We'll use the present value of an ordinary annuity formula, but since it is weekly, we will use the weekly interest rate, and total number of weeks.
Total number of weeks = 40 years * 52 weeks/year = 2080 weeks
Using the present value of an annuity formula:
PV = PMT * [1 - (1 + r)^-n] / r
Where:
* PV = Present Value
* PMT = Weekly payment ($1,700)
* r = Weekly interest rate (0.03 / 52)
* n = Total number of weeks (2080)
PV = 1700 * [1 - (1 + 0.03/52)^-2080] / (0.03/52)
PV = 1700 * [1 - (1.000576923)^-2080] / 0.000576923
PV = 1700 * [1 - 0.301131] / 0.000576923
PV = 1700 * 0.698869 / 0.000576923
PV = 1700 * 1211.37
PV = 2059329
Therefore, the state needs to put approximately $2,059,329 into an account now to cover the weekly prize payments.
**Answers:**
* Total value of the prize: $3,536,000
* Amount needed to cover the prize payments: $2,059,329 (approximately)
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A state lotto has a prize that pays $1,700 each week for 40 years.
(a) Find the total value of the prize: $
Correct
(b) If the state can earn 3% interest on investments, how much money will they need
to put into an account now to cover the weekly prize payments?
~~~~~~~~~~~~~~~~~~~~~~~~
Calculations in the post by @CPhill are incorrect and inaccurate,
as practically always in all his Finance calculations.
In this my post, I present my calculation, which gives different answer.
This problem is about the starting amount of a sinking fund, which pays out $1700
each week during 40 years, compounding weekly at 3% annual interest.
The year is 365/7, or about 52 weeks, so I will use 52 weeks per year.
Use the formula for the monthly payment of a sinking fund
IV = 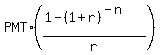 ,
where IV stands for the initial value, PMT is the annual outpayment value,
r is the annual rate, n is the number of payment/compounding (52 times the number of years, in this problem).
With the given data, the formula for calculations is
IV = ,
where IV stands for the initial value, PMT is the annual outpayment value,
r is the annual rate, n is the number of payment/compounding (52 times the number of years, in this problem).
With the given data, the formula for calculations is
IV = 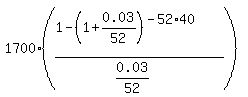 = 2,058,841 dollars.
At this point, I copy-paste this formula into an Excel spreadsheet
without making intermadiate calculations.
Excel spreadsheet is a powerfull calculator. It keeps enough decimal places
to provide the necessary precision. The value, which I got this way is
PV = 2,058,840.57.
ANSWER. The initial/starting value of the fund is about $2,058,841.
This amount is deposited initially, and it provides
no-failure payments of $1,700 at the end of each week during 40 years,
under given conditions.
This initial/starting value of the fund is the "present" value of the prize,
which is won in the lottery.
Notice that the total outpayment in 40 years, under the given condition,
is 40*52*1700 = 3,536,000.
The difference $3,536,000 - $2,058,841 = $1,477,159 is the interest, which the fund earned in 40 years. = 2,058,841 dollars.
At this point, I copy-paste this formula into an Excel spreadsheet
without making intermadiate calculations.
Excel spreadsheet is a powerfull calculator. It keeps enough decimal places
to provide the necessary precision. The value, which I got this way is
PV = 2,058,840.57.
ANSWER. The initial/starting value of the fund is about $2,058,841.
This amount is deposited initially, and it provides
no-failure payments of $1,700 at the end of each week during 40 years,
under given conditions.
This initial/starting value of the fund is the "present" value of the prize,
which is won in the lottery.
Notice that the total outpayment in 40 years, under the given condition,
is 40*52*1700 = 3,536,000.
The difference $3,536,000 - $2,058,841 = $1,477,159 is the interest, which the fund earned in 40 years.
Solved.
----------------------------------
The lesson to learn from this my post is two-fold (1) In such Finance calculations, use powerful enough calculator to provide the necessary precision.
(2) Do not make intermediate rounding ( ! ) Round only the final value ( ! )
|
|
|