Question 1175982: Mike must work at least 18 hours a week to supplement his income while attending school. He has the opportunity to work in two retail stores. In store 1, he can work between 5 and 13 hours a week, and in store 2, he is allowed between 6 and 11 hours. Both stores pay the same hourly wage. In deciding how many hours to work in each store, Mike wants to base his decision on work stress. Based on interviews with present employees, Mike estimates that, on an ascending scale of 1 to 10, the stress factors are 8 and 6 at stores 1 and 2, respectively. Because stress mounts by the hour, he assumes that the total stress for each store at the end of the week is proportional to the number of hours he works in the store. How many hours should Mike work in each store?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! x = the number of hours working at store 1.
y = the number of hours working at store 2.
your constraint functions are:
x + y >= 18
x >= 5
x <= 13
y >= 6
y <= 11
your objective function appears to be total stress factor = 8x + 6y.
this is what you want to minimize.
using the desmos.com calculator, you would graph the opposite of the inequalities of the constraints.
your feasible region is the area on the graph that is not shaded.
you evaluate the objective function at each of the corner points.
the corner points with the smallest value gives you the minimum total stress factor.
the graph looks like this:
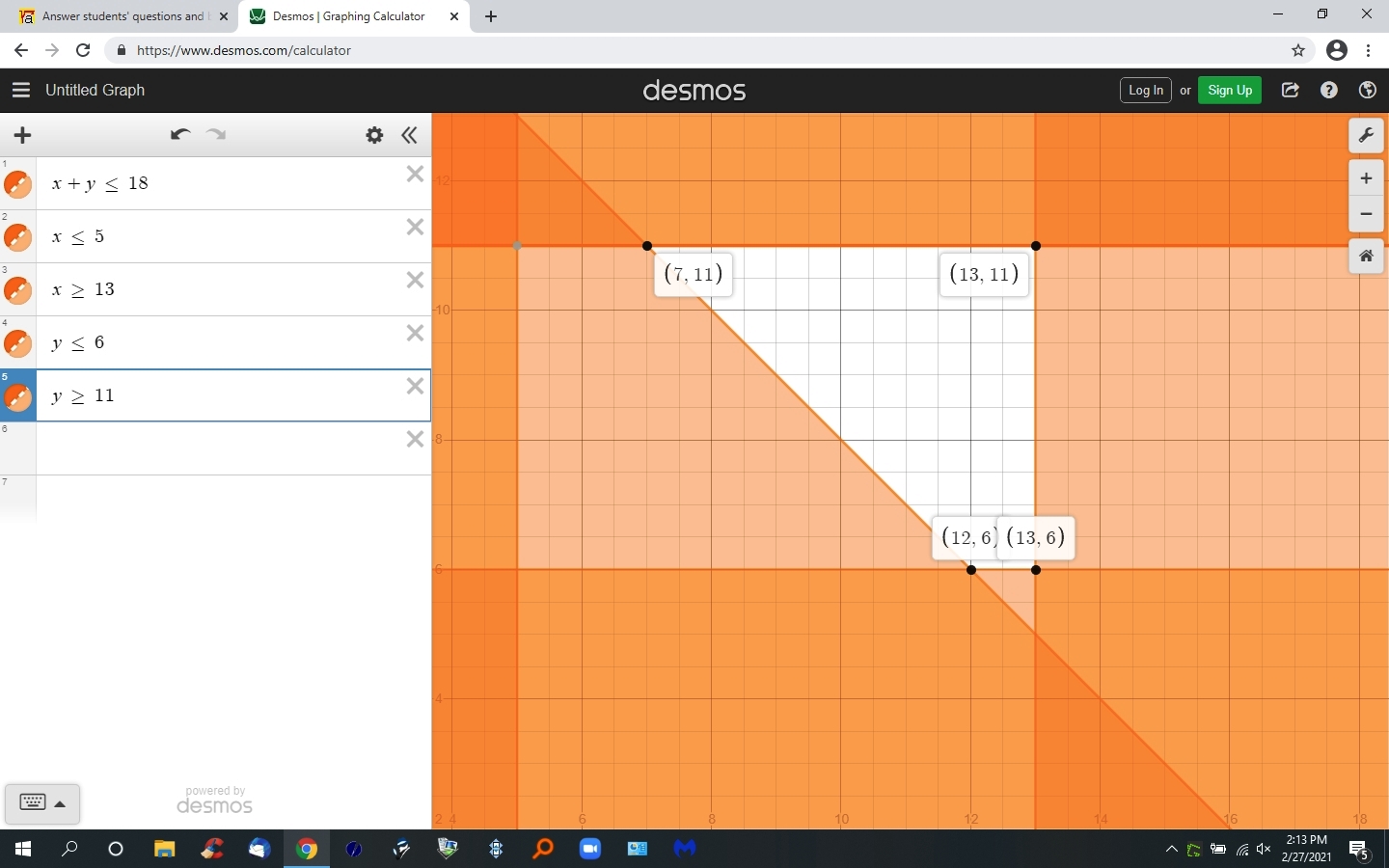
the corner point with the smallest stress factor is (7,11).
the total stress factor there is 122.
all the constraints are satisfied.
x = 7 which is greater than or equal to 5 and less than or equal to 13.
y = 11 which is greater than or equal to 6 and less than or equal to 11.
x + y = 18 which is greater than or equal to 18.
based on this evaluation, he should work 7 hours at store 1 and 11 hours at store 2 to minimize his total stress factor.
|
|
|