Question 1172915: An account provides an interest rate(r) compounded quarterly. At every end of the quarter, $2,500 is deposited. What value of r would make the future value of this account $5,200 in 6 months?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The formula for an Ordinary Annuity saving account compounded quarterly is
FV = 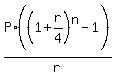 where FV is the future value, P is the annual payment at the end of each year, n is the number of compounding periods.
So, we need to find " r " from the equation
where FV is the future value, P is the annual payment at the end of each year, n is the number of compounding periods.
So, we need to find " r " from the equation
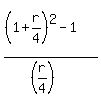 = = 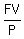 = =  = 2.08.
Multiply both sides by = 2.08.
Multiply both sides by 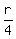 . You will get . You will get
 = =  .
For brevity, introduce new variable x = .
For brevity, introduce new variable x = 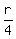 and write this equation in the form and write this equation in the form
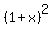 = 1 + 2.08x.
Simplify
1 + 2x + x^2 = 1 + 2.08x
x^2 - 0.08x = 0
x*(x-0.08) = 0.
Of two roots, x= 0 and x= 0.08, only positive root makes sense.
So, x = 0.08; hence r= 4x = 4*0.08 = 0.32.
ANSWER. Annual interest rest should be 0.32, or 32%.
CHECK. = 1 + 2.08x.
Simplify
1 + 2x + x^2 = 1 + 2.08x
x^2 - 0.08x = 0
x*(x-0.08) = 0.
Of two roots, x= 0 and x= 0.08, only positive root makes sense.
So, x = 0.08; hence r= 4x = 4*0.08 = 0.32.
ANSWER. Annual interest rest should be 0.32, or 32%.
CHECK. 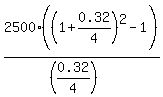 = 5200 dollars. ! Correct ! = 5200 dollars. ! Correct !
Solved, checked, explained and completed.
-----------------------
On ordinary annuity saving plan, see my lessons in this site
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
|
|
|