Question 1172818: Tickets in the ocean park cost 500$ for adults and 400$ for children. The management collected a total amount of not more than 80 000$ from 120 adults and children. What are the possible number of adults and children in the Ocean Park? (find the inequality then GRAPH)
Found 2 solutions by mahikab, ikleyn:
Answer by mahikab(11)   (Show Source): (Show Source):
You can put this solution on YOUR website! Assume number of adults = a and number of children = c
Therefore,
a + c = 120 -------- (1)
and 500a + 400c <= 80000 -----(2)
When c=0, a <= 80000/500 = 160
When a=0, c <= 80000/400 = 200
So, the possible number of adults and children are:
All values of (a, c) satisfying inequation (2) where a <= 160, c <= 200

Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This problem is a SPECIAL CASE: one equation is combined with one inequality.
The equation is
x + y = 120. (x for adults, y for children)
The inequality is
500x + 400y <= 80000
Simplify this inequality by dividing both sides by 100
5x + 4y <= 800.
So, you have, actually, this system (one equation and one inequality)
x + y = 120
5x + 4y <= 800
Also, the problem assumes that both quantities x and y are NON-NEGATIVE
x >= 0, y >= 0.
On the plot, it looks like this
 Plot y = 120-x (red line) and y =
Plot y = 120-x (red line) and y = 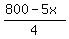 (green line)
The inequality represents all the points inside the triangle in QI under the green line.
The equation represents the red line.
So, the range for x is 0 <= x <= 120.
The range for y is the same 0 <= y <= 120.
But x and y are not independent variables: they are interconnected by the equation x + y = 120.
This plot allows you to see the problem in whole and its solution, in particular.
The solution set is { the INTEGER points of the red line in QI }. (green line)
The inequality represents all the points inside the triangle in QI under the green line.
The equation represents the red line.
So, the range for x is 0 <= x <= 120.
The range for y is the same 0 <= y <= 120.
But x and y are not independent variables: they are interconnected by the equation x + y = 120.
This plot allows you to see the problem in whole and its solution, in particular.
The solution set is { the INTEGER points of the red line in QI }.
It is the full analysis, presented in the form AS IT SHOULD BE DONE.
|
|
|