SOLUTION: Jose paid at Most $250 for the four markers and three pencils that he bought. Suppose the marker is more expensive than the pencil and their price difference is greater than $30. W

    Jose bought 4 identical markers and 3 identical pencils.  He paid at most $250 for his purchase.
    Each marker is $30 more expensive than each pencil. 
    What is the price of the marker and the price of the pencil ?

Let x = the price for each marker,

    y = the number for each pencil.


Then your inequalities are


     4x +  3y <= 250      (1)    (for total)

      x -   y >=  30     (2)    (individual price)


You have a system of inequalities consisting of two inequalities, that must be held simultaneously.


      Use the graphical method to solve it.


In a coordinate plane (x,y) draw the line  y = 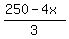, representing first inequality.

Draw the second line  y = x - 30, representing second inequality.


These lines are shown in my plot below.


    


    Plot y = 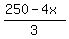  (red),   y = x - 30  (green)


The solution set to your inequalities are the points in the coordinate plane, that are
below or on the red line and below or on the green line.


As you see from the plot, these points belong to a triangle under the red and under the green lines, adjacent to x-axis.