Question 1169752: A tank containing 50 litres of water develops a leak and loses water at a constant rate. After 20 minutes it contains 40 litres. After further 30 minutes the tank is 5% of its full capacity. Determine the tank's capacity.
Answer by ikleyn(52946)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
From first two sentences, we have this equation
V(t) = 50 - a*t.
representing the current volume V(t) as a function of time, t, in minutes,
and "a" is the constant leaking rate in liters per minute.
At t= 20 minutes,
V(20) = 40 = 50 - a*20,
which gives a = 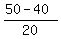 = = 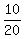 = 0.5 liters per minute.
After further 30 minutes, the volume of the water in the tank is
V(50) = 40 - 0.5*30 = 40 - 15 = 25 liters.
So, 25 liters is 5% of the tank capacity.
Hence, the total capacity of the tank is = 0.5 liters per minute.
After further 30 minutes, the volume of the water in the tank is
V(50) = 40 - 0.5*30 = 40 - 15 = 25 liters.
So, 25 liters is 5% of the tank capacity.
Hence, the total capacity of the tank is 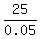 = 500 liters.
ANSWER. The total capacity of the tank is = 500 liters.
ANSWER. The total capacity of the tank is 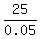 = 500 liters. = 500 liters.
Solved, answered, explained and completed.
|
|
|