Question 1169709: for each of the following, give the amplitude, the period, and describe any vertical or horizontal shifts away from the origin(i.e. from the standard parent graph)
2a f(x) = -2sin[3(x-pi/2)] + 4
b. f(x) = -cos(2x -pi/4) -3
c. f(x) = 2tan(x/3) -1
d. f(x) = -sec(pi- 5x)
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
for each of the following, give the amplitude, the period, and describe any vertical or horizontal shifts
away from the origin(i.e. from the standard parent graph)
2a f(x) = -2sin[3(x-pi/2)] + 4
b. f(x) = -cos(2x -pi/4) -3
c. f(x) = 2tan(x/3) -1
d. f(x) = -sec(pi- 5x)
~~~~~~~~~~~~~~~~~
The analysis given by @MathLover1, has ERRORS, that are extremely dangerous for a beginning student.
Therefore, I came to FIX her errors and to bring a CORRECT ANALYSIS with detailed explanations.
Case (a)
f(x) = -2sin[3(x-pi/2)] + 4.
It is obvious that the amplitude is |-2| = 2 and that the period is  ; vertical shift is 4 units up.
For the further analysis, especially for the accurate analysis of the horizontal shift, you MUST write
the given function with the POSITIVE leading factor (amplitude).
// If you do not make it (as @MathLover1 NEGLECTS do it at every her attempt), you analysis INEVITABLY will be ERRONEOUS. //
So I write equivalent transformations
f(x) = ; vertical shift is 4 units up.
For the further analysis, especially for the accurate analysis of the horizontal shift, you MUST write
the given function with the POSITIVE leading factor (amplitude).
// If you do not make it (as @MathLover1 NEGLECTS do it at every her attempt), you analysis INEVITABLY will be ERRONEOUS. //
So I write equivalent transformations
f(x) = 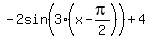 = = 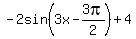 =
I want to make the leading coefficient positive. For it, I continue
= =
I want to make the leading coefficient positive. For it, I continue
=  (I change the leading sign by adding (I change the leading sign by adding  to the sine argument, and then continue further)
= to the sine argument, and then continue further)
= 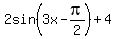 = = 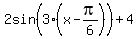 .
Now, having written the sine function in standard CANONIC form with the positive leading coefficient,
I can make the standard analysis for the shift, and I can safely conclude that the horizontal shift is .
Now, having written the sine function in standard CANONIC form with the positive leading coefficient,
I can make the standard analysis for the shift, and I can safely conclude that the horizontal shift is  units to the right.
Now look into the plot below, which CONFIRMS my analysis. units to the right.
Now look into the plot below, which CONFIRMS my analysis.
 Plot y =
Plot y = 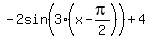 (the given function, red),
and y = sin(3x) (the parent function for the shift analysis, green)
Notice that, when we compare the shift, our reference parent function for the comparison is y = sin(3x), shown by green in my plot. (the given function, red),
and y = sin(3x) (the parent function for the shift analysis, green)
Notice that, when we compare the shift, our reference parent function for the comparison is y = sin(3x), shown by green in my plot.
Case (b)
f(x) = -cos(2x -pi/4) -3.
It is obvious that the amplitude is |-1| = 1 and that the period is  = =  ; vertical shift is 3 units down.
For the further analysis, especially for the accurate analysis of the horizontal shift, you MUST write
the given function with the POSITIVE leading factor (amplitude).
// If you do not make it (as @MathLover1 NEGLECTS do it at every her attempt), you analysis INEVITABLY will be ERRONEOUS. //
So I write equivalent transformations
f(x) = ; vertical shift is 3 units down.
For the further analysis, especially for the accurate analysis of the horizontal shift, you MUST write
the given function with the POSITIVE leading factor (amplitude).
// If you do not make it (as @MathLover1 NEGLECTS do it at every her attempt), you analysis INEVITABLY will be ERRONEOUS. //
So I write equivalent transformations
f(x) = 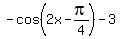 = = 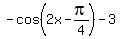 =
I want to make the leading coefficient positive. For it, I continue
= =
I want to make the leading coefficient positive. For it, I continue
= 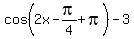 (I change the leading sign by adding (I change the leading sign by adding  to the cosine argument, and then continue further)
= to the cosine argument, and then continue further)
=  = =  .
Now, having written the sine function in CANONIC form with the positive leading coefficient,
I can make the standard analysis for the shift, and I can safely conclude that the horizontal shift is .
Now, having written the sine function in CANONIC form with the positive leading coefficient,
I can make the standard analysis for the shift, and I can safely conclude that the horizontal shift is 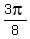 units to the left.
Now look into the plot below, which CONFIRMS my analysis. units to the left.
Now look into the plot below, which CONFIRMS my analysis.
 Plot y =
Plot y = 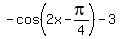 (the given function, red),
and y = cos(2x) (the parent function for the shift analysis, green)
Notice that, when we compare the shift, our reference parent function for the comparison is y = cos(2x), shown by green in my plot. (the given function, red),
and y = cos(2x) (the parent function for the shift analysis, green)
Notice that, when we compare the shift, our reference parent function for the comparison is y = cos(2x), shown by green in my plot.
Case (d)
f(x) = -sec(pi-5x).
In this case, there is NO amplitude. Obviously, the period is 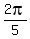 ; there is NO vertical shift.
For the further analysis, especially for the accurate analysis of the horizontal shift, you MUST write
the given function with the POSITIVE leading factor.
So I write equivalent transformations
f(x) = ; there is NO vertical shift.
For the further analysis, especially for the accurate analysis of the horizontal shift, you MUST write
the given function with the POSITIVE leading factor.
So I write equivalent transformations
f(x) = 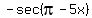 =
I want to make the leading coefficient positive. For it, I change
the leading sign by subtracting =
I want to make the leading coefficient positive. For it, I change
the leading sign by subtracting  to the sec argument, and then continue further
= to the sec argument, and then continue further
= 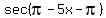 = = 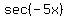 = use the fact that sec is an EVEN function = = use the fact that sec is an EVEN function =  .
Now, having written the sec function in CANONIC form with the positive leading coefficient,
I can make the standard analysis for the shift, and I can safely conclude that the horizontal shift is 0 (zero, ZERO) in this case.
Now look into the plot below, which CONFIRMS my analysis. .
Now, having written the sec function in CANONIC form with the positive leading coefficient,
I can make the standard analysis for the shift, and I can safely conclude that the horizontal shift is 0 (zero, ZERO) in this case.
Now look into the plot below, which CONFIRMS my analysis.
 Plot y =
Plot y = 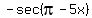 (the given function, red),
and y = sec(5x) + 0.2 (the parent function for the shift analysis, green)
Notice that, when we compare the shift, our reference parent function for the comparison is y = sec(5x), shown by green in my plot.
To make two plots distinguishable, I added 0.2 to the reference function // othewise, the plot are identical and the difference is not seen. (the given function, red),
and y = sec(5x) + 0.2 (the parent function for the shift analysis, green)
Notice that, when we compare the shift, our reference parent function for the comparison is y = sec(5x), shown by green in my plot.
To make two plots distinguishable, I added 0.2 to the reference function // othewise, the plot are identical and the difference is not seen.
==============
At this point, my solution is COMPLETED.
I hope that the reader sees now all errors of the solution by @MathLover1.
She really made all possible and typical errors in her analysis.
I really glad that I had the opportunity to fix all these errors and to teach the reader TO AVOID them.
|
|
|