Question 1169054: Help please,this is a situational problem about parabola that I find hard to answer. Each cable of a suspension bridge is in the shape of a parabola and is supported by two towers at each end. The shape of the cable is modeled by the equation x^2=200y,where x and Y are measured in meters. Find the coordinate of the focus. Thank you so much in advance!
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the equation is 200y = x^2
divide both sides of the equation by 200 to get:
y = 1/200 * x^2
the equation is now in standard form.
the vertex form of the equation for a parabola is:
y = a * (x-h)^2 + k
(h,k) is the coordinates of the vertex of the parabola.
a is the coefficient of the x^2 term.
the vertex of your quadratic equation is at the point (0,0).
the value of a is 1/200.
plug these numbers into the vertex form of the equation to get:
y = 1/200 * (x - 0)^2 + 0
the coordinate of the focus are at (h,k + 1/4a)
this makes the coordinate of the focus at (0,0 + 1/(4/200))
simplify this to get:
the coordinate of the focus is as (0,50).
the focus is on the axis of symmetry.
the distance from the focus to the vertex is the same distance from the directrix to the vertex.
this makes the equation of the line of the directrix y = -50.
one of the properties of a parabola is that the distance from the focus to any point on the parabola is the same distance from any point on the parabola to the directrix.
i verified that this is true from two sample points.
you can do the same.
just calculate the distance between the focus and any point on the parabola and then calculate the distance from that point to the directrix.
the distance from any point on the parabola to the directrix is a vertical line from that point to the directrix, assuming the parabola is a vertical parabola, such as the one in your problem.
i graphed your parabola and i graphed the focus and the directrix.
you can you calculate the distance between the focus (0,50) and the chosen point on the parabole (200,200), and you can calculate the distance between the chosen point on the parabola and the point on the directrix (200,-50).
you will see that the distances are the same.
if you do it correctly, the distances should be the same with a value of sqrt(62500)
here's my graph.
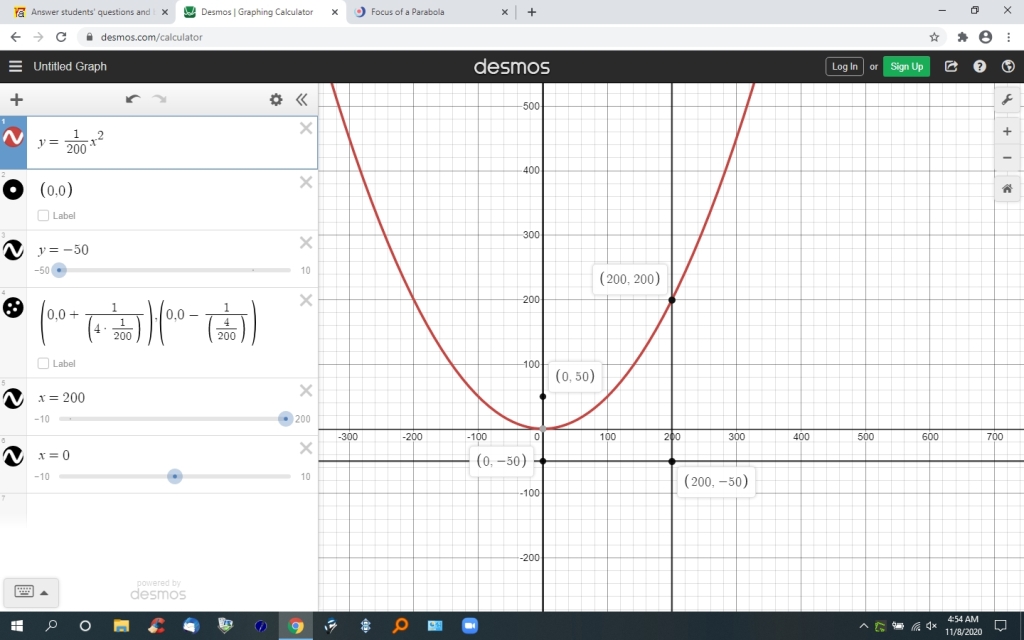
here's some references.
https://www.varsitytutors.com/hotmath/hotmath_help/topics/focus-of-a-parabola#:~:text=A%20parabola%20is%20set%20of,of%20symmetry%20of%20the%20parabola.
https://courses.lumenlearning.com/waymakercollegealgebra/chapter/characteristics-of-parabolas/
https://www.mathsisfun.com/geometry/parabola.html
https://www.purplemath.com/modules/parabola.htm
|
|
|