.
If A = (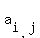 ) and B = (
) and B = (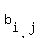 ), then
(A,B) = tr(A^t * B) =
), then
(A,B) = tr(A^t * B) = 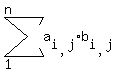 .
From it, it is easy to deduce that the orthogonal complement of the subspace of all DIAGONAL matrices
is the subspace of the matrices with the zero trace { A = (
.
From it, it is easy to deduce that the orthogonal complement of the subspace of all DIAGONAL matrices
is the subspace of the matrices with the zero trace { A = (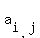 ) |
) |  }. ANSWER
Similarly, it is easy to deduce that the orthogonal complement of space of symmetric matrices is the space of all skew-symmetric matrices.
}. ANSWER
Similarly, it is easy to deduce that the orthogonal complement of space of symmetric matrices is the space of all skew-symmetric matrices.