Question 1164370: Jane and Tom had some sweets each. Jane gave 1/2 of what she had to Tom. Then Tom gave 1/3 of what he had to Jane. Jane then gave 1/2 of what she had to Tom. As a result Jane had 54 sweets and Tom had150 sweet. How many sweets did Tom have at first?
Found 2 solutions by Theo, MathTherapy:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let x equal the amount of sweets that jane had to start.
let y equal the amount of sweets that tom had to start.
jane has x sweets to start.
tom has y sweets to start.
jane give half of her sweets to tom.
she give him .5 * x
she now has .5 * x sweets.
tom accepts the sweets from jane.
he adds that to his pile of sweets.
he had y sweets before she gives him her s.
tom gives jane 1/3 of his sweets.
he gives her 1/3 * (1/2 * x + y) sweets.
simplify that to get:
he gives her 1/6 * x + 1/3 * y sweets.
he is left with 2/3 * (1/2 * x + y) sweets.
simplify that to get:
he is left with 1/3 * x + 2/3 * y sweets.
jane accepts the sweets from tom.
she had .5 * x sweets.
she adds 1/6 * x + 1/3 * y sweets to that.
she now has .5 * x + 1/6 * x + 1/3 * y sweets.
simplify that to get:
she now has 2/3 * x + 1/3 * y sweets.
she gives half of her sweets again to tom.
she has 2/3 * x + 1/3 * y sweets
she gives half of that to tom.
she gives him 1/3 * x + 1/6 * y sweets
she has 1/3 * x + 1/6 * y sweets remaining.
tom receives the half of her sweets.
he had 1/3 * x + 2/3 * y sweets before the gift.
he now has 1/3 * x + 2/3 * y + 1/3 * x + 1/6 * y sweets remaining.
combine like terms and simplify that to get:
he now has 2/3 * x + 5/6 * y remaining.
the total that jan now has is 1/3 * x + 1/6 * y sweets.
this is equal to 54.
jane's equation becomes:
1/3 * x + 1/6 * y = 54
the total that tom now has is 2/3 * x + 5/6 * y
this is equal to 150.
tom's equation becomes:
2/3 * x + 5/6 * y = 150
you have two equations that need to be solved simultaneously.
they are:
1/3 * x + 1/6 * y = 54
2/3 * x + 5/6 * y = 150
multiply the first equation by 2 and leave the second equation as is to get:
2/3 * x + 2/6 * y = 108
2/3 * x + 5/6 * y = 150
subtract the first eqution from the second to get:
1/2 * y = 42
solve for y to get:
y = 84
replace y with 84 in the first original equation to get:
first original equation was 1/3 * x + 1/6 * y = 54
replace y with 84 to get:
1/3 * x + 1/6 * 84 = 54
simplify to get:
1/3 * x + 14 = 54
solve for x to get:
x = 3 * (54 - 14) = 3 * 40 = 120
you now have:
x = 120 and y = 84
this means jane had 84 sweets to start with and tom had 120 sweets to start with.
to confirm, go through the problem again with these values.
jane has 120 to start with.
she give tom half.
she gives him 60
she has 60 remaiining.
tom has 84 to start with
he gets 60 from jane.
he now has 144.
tom gives 1/3 of his sweets to jane.
he gives her 1/3 * 144 = 48
he has 144 - 48 = 96 remaining.
jane gets 48 from tom.
she now has 60 + 48 = 108.
jane gives half of these back to tom.
she give him 54.
she has 54 left.
tom gets 54 from jane.
he now has 96 + 54 = 150 remaining.
jane winds up with 54 after all is done.
tom winds up with 150 after all is done.
this confirms the solution is good.
the solution is that tom had 84 sweets to start with.
Answer by MathTherapy(10559)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Jane and Tom had some sweets each. Jane gave 1/2 of what she had to Tom. Then Tom gave 1/3 of what he had to Jane. Jane then gave 1/2 of what she had to Tom. As a result Jane had 54 sweets and Tom had150 sweet. How many sweets did Tom have at first?
Let number that Tom and Jane had, at 1st be T, and J, respectively
After giving ½ to Tom, Jane had ½J, or 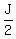 left
After getting ½ from Jane, Tom had left
After getting ½ from Jane, Tom had 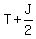 After giving
After giving  to Jane, Tom had to Jane, Tom had 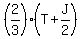 , or , or 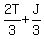 left
After getting left
After getting  from Tom, Jane had from Tom, Jane had 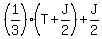 , or , or  , or , or  , left
After giving ½ to Tom, Jane had ½ * , left
After giving ½ to Tom, Jane had ½ * 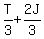 , or , or 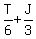 , left
After getting ½ from Jane, Tom had , left
After getting ½ from Jane, Tom had  We now have:
We now have:  5T + 4J = 900 ---- Multiplying by LCD, 6 ------- eq (i)
Also,
5T + 4J = 900 ---- Multiplying by LCD, 6 ------- eq (i)
Also,  T + 2J = 324 ---- Multiplying by LCD, 6 ------- eq (ii)
- 2T - 4J = - 648 -- Multiplying eq (ii) by - 2 -- eq (iii)
3T = 252 ---- Adding eqs (iii) & (i)
Number of sweets Tom had, at first, or
T + 2J = 324 ---- Multiplying by LCD, 6 ------- eq (ii)
- 2T - 4J = - 648 -- Multiplying eq (ii) by - 2 -- eq (iii)
3T = 252 ---- Adding eqs (iii) & (i)
Number of sweets Tom had, at first, or 
|
|
|