SOLUTION: What is the recursive formula of 1/5, 2/7, 4/9, 8/11, 16/13

1/5, 2/7, 4/9, 8/11, 16/13

2nd term divided by 1st term = (2/7)/(1/5) = (2/7)∙(5/1) = 10/7

3rd term divided by 2nd term = (4/9)/(2/7) = (4/9)∙(7/2) = 14/9

4th term divided by 3rd term = (8/11)/(4/9) = (8/11)∙(9/4) = 18/11

5th term divided by 4th term = (16/13)/(8/11) = (2/7)∙(11/8) = 22/13

So

To get the 2nd term, we multiply the 1st term by 10/7

To get the 3rd term, we multiply the 2nd term by 14/9

To get the 4th term, we multiply the 3rd term by 18/11

To get the 5th term, we multiply the 4th term by 22/13

The general term of those numerators for terms n=2,3,4,5,6
are 10,14,18,22 is 4n+2

The general term of those denominators for terms n=2,3,4,5,6
are 7,9,11,13 is 2n+3.


So we multiply each term by 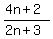 to get the next term.

Recursive formula:

,    

Edwin