Question 1160362: A boy has $3.70 in dimes and quarters. If the dimes were quarters, and the quarters were dimes, the money would have been $4.00. How many coins does the boy have?
Found 3 solutions by ikleyn, greenestamps, josgarithmetic:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A boy has $3.70 in dimes and quarters. If the dimes were quarters, and the quarters were dimes,
the money would have been $4.00. How many coins does the boy have?
~~~~~~~~~~~~~~~~~
From the condition, you have these two equations
10d + 25q = 370 (1)
25d + 10q = 400 (2)
Multiply equation (1) by 5 (both sides). Multiply equation (2) by 2 (both sides)
50d + 125q = 1850 (3)
50d + 20q = 800 (4)
Subtract equation (4) from equation (2)
105q = 1850 - 800 = 1050.
q = 1050/105 = 10.
Then from equation (1), d = (370-25*10)/10 = 12
ANSWER. There are 12 dimes and 10 quarters. The total number of coins is 22.
------------
Another way to find the total number of coins is to add equations (1) and (2).
You will get then
35d + 35q = 370 + 400
35*(d + q) = 770
d + q = 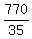 = 22. = 22.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Thanks for re-posting the problem with the correct description.
Here is the way I would solve the problem by a somewhat unorthodox method. You will probably get responses from other tutors showing more standard solution methods.
(1) The value of the coins increases from $3.70 to $4.00 when the dimes and quarters are switched -- an increase of 30 cents.
(2) The difference between the value of a dime and the value of a quarter is 15 cents.
(3) That means the number of quarters after the switch is 30/15 = 2 more than the number of dimes; that of course means with the actual coins the number of dimes is 2 more than the number of quarters.
So we have $3.70 in dimes and quarters, with 2 more dimes than quarters.
(4) Take away those two "extra" dimes and we have equal numbers of dimes and quarters with a total value of $3.70-$0.20 = $3.50.
(5) The value of one quarter and one dime is $0.35.
(6) The number of quarters and dimes (after we took away the two "extra" dimes) is $3.50/$0.35 = 10.
(7) Now bring back those two "extra" dimes to get the actual numbers of coins.
ANSWER: 10 quarters and 12 dimes; 22 coins total
-----------------------------------------------------------
In the solution above, I blindly plunged in to solving the problem thinking that I needed to determine the number of dimes and the number of quarters. But the problem doesn't ask us to do that. It only asks us to find the total number of coins.
In that case, there is an almost trivial path to the solution.
The total value of the coins is $3.70; and when the dimes and quarters are switched, the value is $4.00.
Add those two and we get that double the value of the coins is $7.70, and the numbers of quarters and dimes are now the same.
Then, since the value of one quarter and one dime is $0.35, the number of coins is $7.70/($0.35) = 22.
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
|
|
|