Question 1152549: Find the equation of the line with the given properties. Express each in the standard form. Sketch the lines. Parallel to the y-axis and passing through (5,-7).
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the equation of a line parallel to the y-axis and passing through the point (5,-7) is x = 5.
since the line is vertical, then all points on the line will have the x-coordinate of 5.
the standard form of the equation of a straight line is ax + by = c.
if the line is vertical, then the coefficient of the y term is equal to 0 and he equation becomes ax = c
if you solve for x, then you get x = c/a.
if the equation of the line is x = 5, then you get c/a = 5.
this means that any value of c divided by a must be equal to 5.
for example:
if a = 1, then c = 5
if a = 2, then c = 10
if a = 3, then c = 15
etc.
when you simplify all these forms, you always wind up with x = 5.
for example:
3x = 15 simplifies to x = 15/3 = 5.
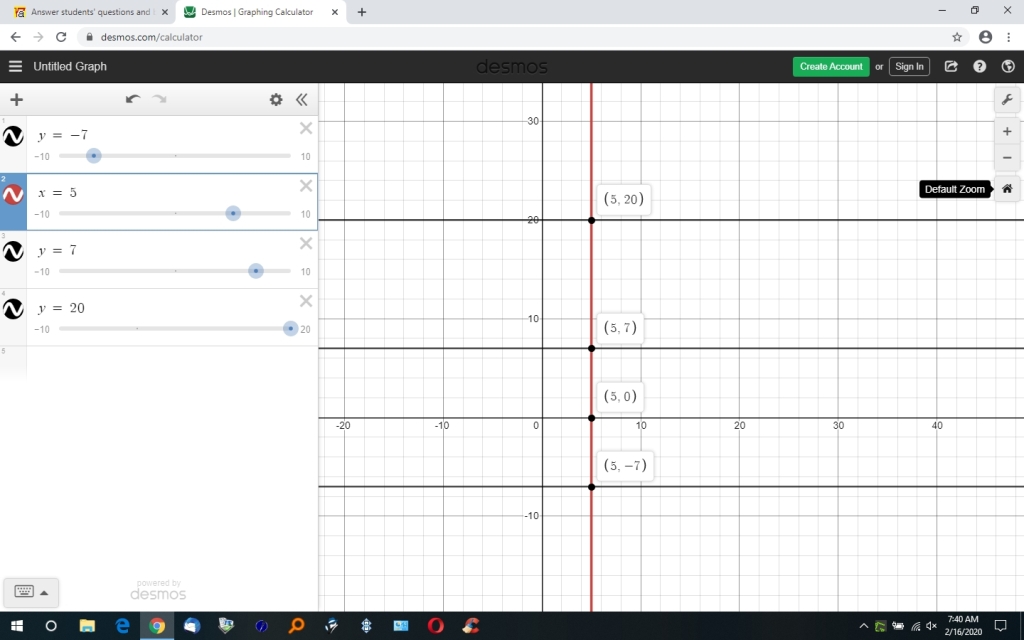
if you graph the line x = 5, you will see that all possible points on the line each have the x-coordinate of 5.
the point (5,-7) is just one of these points on the line with the x-coordinate of 5.
here's a graph of the line with a select few other points on the line as well.
|
|
|