Question 1148381: The probability of winning a prize in a game of chance is 0.48. What is the least number of games that must be
played to ensure that the probability of winning at least twice is more than 0.95?
Answer by greenestamps(13219)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Think of the problem as finding the least number of games that must be played so that the probability of NOT winning at least twice (i.e., the probability of winning either 0 or 1 times) is LESS THAN 1-.95 = .05.
Many calculators have the capability of computing probabilities like this. On the TI-83/84, 2nd-VARS-binomcdf can be used.
The probability of NOT winning (which is what we are now working with) is 0.52. The probability of not winning at most 1 time on n trials, with a probability of 0.52, is calculated on the TI-83 with the input
binomcdf(n,.48,1)
Of course, you need to enter a value for n, so you need to do the calculation several times, starting with small numbers, and increasing the number of trials until the value obtained is less than .05.
It turns out that on the TI-83 you can also define a function binomcdf(x,.48,1) and use the TBLSET and TABLE features to find the smallest value of x for which the probability is less than 05.
Finally, if you don't have a calculator that will compute cumulative probabilities, you can use the function that directly calculates the probability of losing only 0 or 1 times in x trials.
The probability of losing is 0.52 and the probability of not losing is 0.48.
The probability of winning 0 times in x trials is
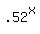
The probability of winning 1 time in x trials is
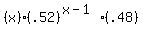
So the function to calculate the probability of winning LESS THAN 2 times on x trials is
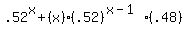
On a graphing calculator, graph this function and the constant function .05 and see where they intersect. The answer to the problem is the least integer greater than the value of x where the graphs intersect.
|
|
|