Question 1146641: the mean month electric bill for a complex of apartments is r1800. assuming that the bills are normally distributed with a standard distribution of r250, approximately what percentage of these apartments have monthly bills in excess of r2000
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the mean is 1800 and the standard deviation of 250.
you want to know the percent of apartments that have monthly bills in excess of 2000.
the difference between 2000 and 1800 is 200.
divide that by 250 and you get a z-score of (2000 - 1800) / 250 = .8
that's because the z-score formula is z = (x-m)/s
z is he z-score.
x is the raw score.
m is the mean.
s is the standard deviation, in this case.
with a z-score of .8, the area to the left of it is equal to .7881446663.
that means the area to the right of it is equal to 1 minus that = .2118553337.
multiply that by 100 to get 21.18553337%.
round to 2 decimal places to get 21.19%.
that's the percent of apartments that have monthly bills in excess of 2000.
these results were found manually.\
they are supported by results from the online calculator at https://www.omnicalculator.com/statistics/normal-distribution, shown below.
they are visually supported by results from the online calculator at http://davidmlane.com/hyperstat/z_table.html, shown below that.
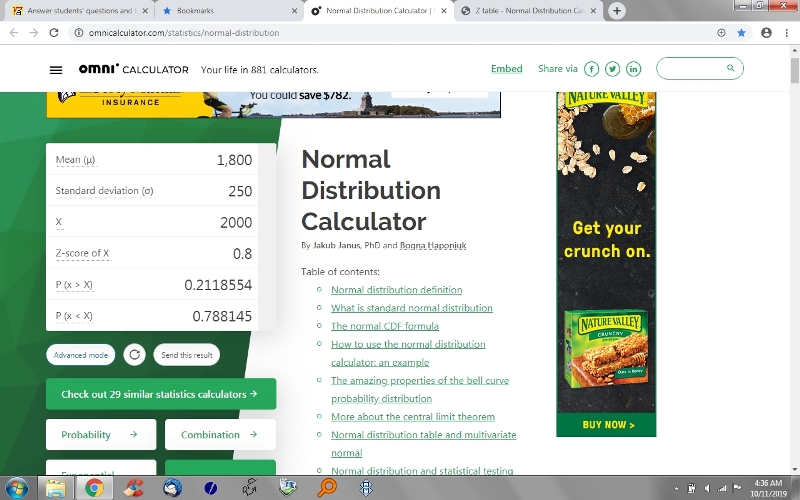
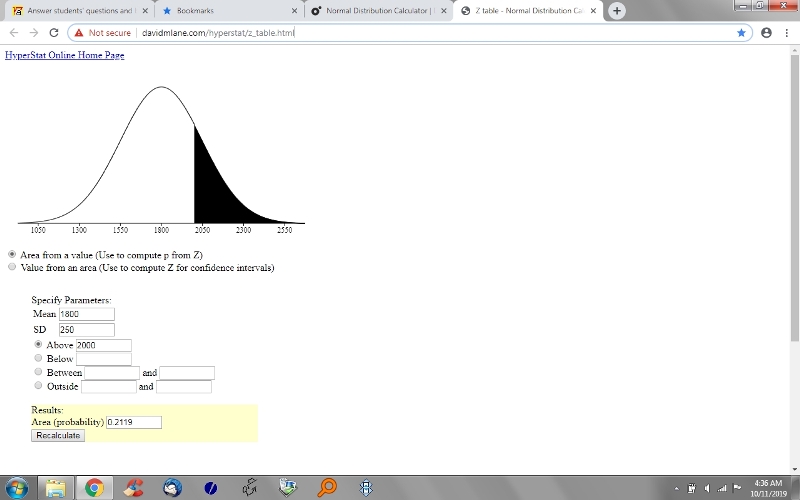
p(x>X) is the area to the right of the z-score of .8
p(x
the visual display is showing you the raw score, not the z-score.
if you used that calculator with z-scores, then the mean would have to be 0 and the standard deviation would have to be 1 and you would be looking for the area above the z-score of .8.
the value for the probability (area above .8) would be the same as shown when using the raw scores.
you have the links, so you can try that out for yourself.
in the first display, i entered mean, standard deviation, and X.
the calculator did the rest.
this could also have been done using the normal distribution tables, but the answer wouldn't have been as accurate and it would have required more work.
if you need to know how to do that, send me an email and i'll show you how it's done.
|
|
|