SOLUTION: Maria have NINE NUMBERS 1, 2,3,4,5,6,7,8 and 9 she adds 2 to some of them and 5 to the others.what is the smallest number of different results she can obtain?

Let "a" denotes any number of the set {1,2,3,4,5,6,7,8,9}, and let "b" denotes any number of the same set.


Maria forms new numbers a'= a+2 and b'= b+5.  She wants to select some subset A for "a"s 
(and automatically to get its complement B for "b"s)

in a way that the number of distinct differences a'-b' would be minimal.


The difference a'-b' is 

    a' - b' = (a+2) - (b+5) = (a-b) - 3.


So, she actually wants to select the subset A and its complement B in a way to have MAXIMUM possible 
number of solutions of the equation

    a - b = 3.


In other terms, she wants to have maximum possible number of pairs (a,b), "a" belongs to A, "b" belongs to B = 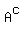 with  a - b = 3.


Now, after this series of reformulations, the answer is OBVIOUS:

    take the pairs (a,b), where "a" is 3 units greater than "b", and try to collect maximum possible number of such pairs.


My answer is:  A = {4, 5, 6} U {7,8,9},

               B = {1, 2, 3}. 


So, my A is the union of two subsets,  X = {4, 5, 6}  and Y = {7,8,9}.


In all, she will have 6*3 = 18 different pairs (a',b');  of them,  3 pairs will give zero difference (a'-b'). 

These three pairs are (4,1), (5,2) and (6,3).


At this selection, the number of pairs with NON-ZERO difference (a'-b') is 18-3 = 15, and, according 
to the solution, this number is maximal.


Notice that the solution, i.e. selection/choice of sets A and B is not unique.

Maria can select them in different way, but can not make "the number of different results" smaller.

Still I think that the problem formulation is incomplete and missed something.


    For example, she can put A = {1,2,3,4,5,6,7,8,9} and B = {empty}.

    Then the number of pairs and differences is 0 (zero, ZERO).   (!)



    Another choice is to select A of 8 elements and B (as the complement) of only 1 element.
    Then the number of different pairs is 8 --- very small, but the mathematical meaning of the problem totally disappears. 


    Third choice is to select A of 7 elements and B of remaining 2 elements.
    Then the number of different pairs is 7*2 = 14 only (!), but the the mathematical meaning of the problem 
    disappears, again (at least, in half).