Question 1143014: If x+y+z=16 then find the maximum value of (x-3)(y-5)(z-2). Given that (x-3)>0, (y-5)>0, (z-2)>0
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20067)   (Show Source): (Show Source):
Answer by ikleyn(52946)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
By analogy with the well known AM-GM inequality ("Arithmetic Mean - Geometric Mean inequality") for two variables "a" and "b"
ab <= 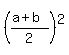 , (1)
there is AM-GM inequality for three variables "a", "b" and "c"
abc <= , (1)
there is AM-GM inequality for three variables "a", "b" and "c"
abc <=  . (2)
Inequalities (1) and (2) are valid for any two and three variables, respectively, that are real non-negative numbers.
Apply inequality (2), taking
a = x-3, b = y-5, c = z-2.
You will get
(x-3)*(y-5)*(z-2) <= . (2)
Inequalities (1) and (2) are valid for any two and three variables, respectively, that are real non-negative numbers.
Apply inequality (2), taking
a = x-3, b = y-5, c = z-2.
You will get
(x-3)*(y-5)*(z-2) <= 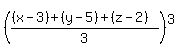 = = 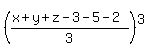 = = 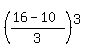 = = 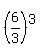 = =  = 8.
Thus for any 3 values of x, y and z, restricted by the equality
x + y + z = 16 and inequalities x >= 3, y >= 5 and z >= 2,
the inequality
(x-3)*(y-5)*(z-2) <= 8
is held.
From the other side, at x= 5, y= 7 and z= 4 we have
(x-3)*(y-5)*(z-2) = (5-3)*(7-5)*(4-2) = 2*2*2 = 8.
and the values of x, y and z satisfy all needed restrictions.
Thus the maximum value of (x-3)*(y-5)*(z-2), where x, y and z are restricted by
x + y + z = 16, x >= 3, y >= 5 and z >= 2
is 8. ANSWER = 8.
Thus for any 3 values of x, y and z, restricted by the equality
x + y + z = 16 and inequalities x >= 3, y >= 5 and z >= 2,
the inequality
(x-3)*(y-5)*(z-2) <= 8
is held.
From the other side, at x= 5, y= 7 and z= 4 we have
(x-3)*(y-5)*(z-2) = (5-3)*(7-5)*(4-2) = 2*2*2 = 8.
and the values of x, y and z satisfy all needed restrictions.
Thus the maximum value of (x-3)*(y-5)*(z-2), where x, y and z are restricted by
x + y + z = 16, x >= 3, y >= 5 and z >= 2
is 8. ANSWER
--------------
S O L V E D.
|
|
|