I'll only do one. I'll do (v)
 Get terms in x² and x together. Since there is no term in y, write y² as
(y-0)²
Get terms in x² and x together. Since there is no term in y, write y² as
(y-0)²
 Factor the coefficient of x² out of the x² and the x terms.
Factor the coefficient of x² out of the x² and the x terms.
 Add and subtract 1 inside the first parentheses:
Add and subtract 1 inside the first parentheses:
 Factor the first three terms inside the first parentheses:
Factor the first three terms inside the first parentheses:
 Distribute the 4 into the big parentheses, removing the big parentheses,
leaving the smaller parentheses intact:
Distribute the 4 into the big parentheses, removing the big parentheses,
leaving the smaller parentheses intact:
 Add 4 to both sides
Add 4 to both sides
 Get 1 on the right side by dividing every term by 100
Get 1 on the right side by dividing every term by 100
 Simplify to get in standard form:
Simplify to get in standard form:
 Since x comes first, the hyperbola opens left and right.
Compare to equation
Since x comes first, the hyperbola opens left and right.
Compare to equation  a² = 25, so a = 5; b² = 4, so b = 2
Center = (h,k) = (1,0), semi-transverse axis = a = 5,
semi-conjugate axis = b = 2
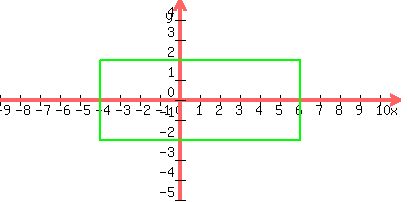
Draw defining rectangle with center (h,k) = (1,0) with horizontal dimension
equal to the entire transverse axis, or 2a = 2(5) = 10 units and vertical
dimension equal to the the entire conjugate axis, or 2b = 2(2) = 4.
a² = 25, so a = 5; b² = 4, so b = 2
Center = (h,k) = (1,0), semi-transverse axis = a = 5,
semi-conjugate axis = b = 2
Draw defining rectangle with center (h,k) = (1,0) with horizontal dimension
equal to the entire transverse axis, or 2a = 2(5) = 10 units and vertical
dimension equal to the the entire conjugate axis, or 2b = 2(2) = 4.
 Draw and extend the diagonals of the defining rectangle. They are the
asymptotes.
Draw and extend the diagonals of the defining rectangle. They are the
asymptotes.
 Now we can sketch in the hyperbola.
Now we can sketch in the hyperbola.
 The vertices are the midpoints of the left and right sides of the defining
rectangle, (-4,0) and (6,0).
We calculate the foci, by using the Pythagorean relationship for all
hyperbolas, which is c²=a²+b², where c is the distance from the center to
the foci.
The vertices are the midpoints of the left and right sides of the defining
rectangle, (-4,0) and (6,0).
We calculate the foci, by using the Pythagorean relationship for all
hyperbolas, which is c²=a²+b², where c is the distance from the center to
the foci.





 , approximately
The word "foci" is the plural of the word "focus".
The left focus is c units left of the center (1,0) or
, approximately
The word "foci" is the plural of the word "focus".
The left focus is c units left of the center (1,0) or 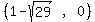 The right focus is c units right of the center (1,0) or
The right focus is c units right of the center (1,0) or 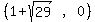 They are the two black dots drawn below:
They are the two black dots drawn below:
 To find the equations of the asymptotes, they are the lines that go:
(1) through the center (1,0) and the upper right corner of the defining
rectangle (6,2), which has slope 2/5, which is b/a, so the equation is
To find the equations of the asymptotes, they are the lines that go:
(1) through the center (1,0) and the upper right corner of the defining
rectangle (6,2), which has slope 2/5, which is b/a, so the equation is


 (2) through the center (1,0) and the lower right corner of the defining
rectangle (6,-2), which has slope -2/5, which is -b/a, so the equation is
(2) through the center (1,0) and the lower right corner of the defining
rectangle (6,-2), which has slope -2/5, which is -b/a, so the equation is


 Edwin
Edwin