SOLUTION: In a particular math class, an instructor is giving a 15 question "true or false" quiz and the sequence of correct and incorrect answer is observed. A monkey strolls into the class

Algebra ->  Finance -> SOLUTION: In a particular math class, an instructor is giving a 15 question "true or false" quiz and the sequence of correct and incorrect answer is observed. A monkey strolls into the class      Log On


   

Question 1138983: In a particular math class, an instructor is giving a 15 question "true or false" quiz and the sequence of correct and incorrect answer is observed. A monkey strolls into the class grabs a quiz from the instructor, sits down and randomly selects either true or false for each of the questions, hands the completed quiz to the bewildered instructor, and walks out the classroom. Calculate the probabilities, should have four decimal place accuracy.
a.) What is the probability that the monkey will get less than 75% on the quiz?
b.) Which situation (situation 1 or 2) has the higher probability of occurring, situation 1: the monkey either gets 3,6, or 8 correct answers or situation 2: the monkey either gets 5,6, or 9 correct answers.
Answer by VFBundy(438) About Me  (Show Source):
You can put this solution on YOUR website!
a.) What is the probability that the monkey will get less than 75% on the quiz?

75% of 15 correct answers is 11.25 answers. Therefore, we are being asked what the probability is that the monkey gets 11 or fewer correct answers. The easiest way to do this is to figure out the probability the monkey gets 12 or more correct answers, then subtract this result from 1.

Probability of exactly 15 correct answers: 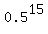0.5%5E15 = 0.00003
Probability of exactly 14 correct answers: %280.5%5E14%29%2A%280.5%5E1%29%2A%2815%21%2F%2814%21%2A1%21%29%29 = 0.00046
Probability of exactly 13 correct answers: %280.5%5E13%29%2A%280.5%5E2%29%2A%2815%21%2F%2813%21%2A2%21%29%29 = 0.00320
Probability of exactly 12 correct answers: %280.5%5E12%29%2A%280.5%5E3%29%2A%2815%21%2F%2812%21%2A3%21%29%29 = 0.01389

Probability of 12 or more correct answers: 0.00003 + 0.00046 + 0.00320 + 0.01389 = 0.01758

Probability of 11 or fewer correct answers: 1 - 0.01758 = 0.98242. (Rounded off to four decimals, the answer is 0.9824.)

b.) Which situation (situation 1 or 2) has the higher probability of occurring, situation 1: the monkey either gets 3,6, or 8 correct answers or situation 2: the monkey either gets 5,6, or 9 correct answers.

Situation 1:
Probability of exactly 3 correct answers: 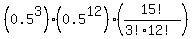%280.5%5E3%29%2A%280.5%5E12%29%2A%2815%21%2F%283%21%2A12%21%29%29 = 0.01389
Probability of exactly 6 correct answers: 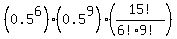%280.5%5E6%29%2A%280.5%5E9%29%2A%2815%21%2F%286%21%2A9%21%29%29 = 0.15274
Probability of exactly 8 correct answers: 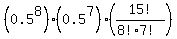%280.5%5E8%29%2A%280.5%5E7%29%2A%2815%21%2F%288%21%2A7%21%29%29 = 0.19638

Probability of either 3, 6, or 8 correct answers: 0.01389 + 0.15274 + 0.19638 = 0.36301

Situation 2:
Probability of exactly 5 correct answers: %280.5%5E5%29%2A%280.5%5E10%29%2A%2815%21%2F%285%21%2A10%21%29%29 = 0.09164
Probability of exactly 6 correct answers: 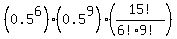%280.5%5E6%29%2A%280.5%5E9%29%2A%2815%21%2F%286%21%2A9%21%29%29 = 0.15274
Probability of exactly 9 correct answers: %280.5%5E9%29%2A%280.5%5E6%29%2A%2815%21%2F%289%21%2A6%21%29%29 = 0.15274

Probability of either 5, 6, or 9 correct answers: 0.09164 + 0.15274 + 0.15274 = 0.39712

Situation 2 has the higher probability of occurring.