.
The formulation of the problem in the post leaves the room for questions
is 100 included ? Is 1000 included ?
In this sense, this formulation is unprofessional. A professional formulation of a Math problem does not leave
the room for such questions. Therefore, I will reformulate the problem in this way:
How many three-digit numbers are
- Not divisible by 2 ?
- Not divisible by 3 ?
- Not divisible by either 2 or 3 ?
Thre-digit numbers are the numbers from 100 to 999 inclusively, so there is no uncertainty with this formulation.
(a) How many three-digit numbers are not divisible by 2 ?
Every second integer number in the interval [100,999] is divisible by 2.
The number of such pairs is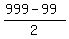 
= 
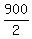= 450.
So, 450 of the 900 numbers are divisible by 2, and the rest, 900-450 = 450 ARE NOT divisible by 2. ANSWER
(b) How many three-digit numbers are not divisible by 3 ?
Every third integer number in this interval is divisible by 3.
More precisely, every third, starting from 102.
The number of such triples is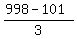 
= 299.
To it, I must add 1 to account for the number 999, which goes individually, without companions.
So, 300 = 299+1 of the 900 numbers are divisible by 3, and the rest, 900-300 = 600 ARE NOT divisible by 3. ANSWER
(c) How many three-digit numbers are not divisible by either 2 or 3 ?
As a first approach, we can subtract 450 and 300 from 900 - those integer numbers that are divisible by 2 and by 3.
900 - 450 - 300 = 150.
But doing in this way, we subtract multiples of 6 twice (!).
Therefore, we must return back the number of multiples of 6 among 3-digit numbers.
Again, we need to calculate the number of segments of the length 6 from 100 to 999 inclusively.
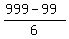= 150.
Hence, the number of multiples to 6 between 100 and 999 is 150.
Therefore, our final answer to question (c) is 150 + 150 = 300. ANSWER
Solved.
