Question 1137224: I need help with the equations.
Find the equation of the line given the following conditions.
6. Passing through (-8, -10) and parallel to the line whose equation is y = -4x + 3
7. Passing through (2, -3) and perpendicular to the line whose equation is y = (1/5) x + 6
8. Passing through (5, -9) and perpendicular to the line whose equation is x + 7y - 12 = 0
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! when doing problem such as this, it's best to convert the equation to slope intercept form.
slope intercept form is y = mx + b
m is the slope and b is the y-intercept.
once you have your equations in this form, then the following rules apply.
if the slopes are identical and the y-intercepts are different, then the lines are parallel.
if the slopes are identical and the y-intercepts are identical, then the lines are equivalent meaning they represent the same line.
if the slopes are negative reciprocals of each other than the lines are perpendicular to each other.
if the slopes are not identical and the slopes are not negative reciprocals of each other, then the lines are not parallel to each other and not perpendicular to each other and they will intersect.
parallel lines never intersect so there are no common points between them.
equivalent lines are the same line so there are an infinite number of common points between them.
lines that are perpendicular to each other will intersect in one point.
lines that are not parallel to each other nor identical (equivalent) to each other will also intersect in one point.
here's a reference.
https://www.montereyinstitute.org/courses/Algebra1/COURSE_TEXT_RESOURCE/U06_L1_T1_text_final.html
now to your problems.
----------------------------------------------------------------------
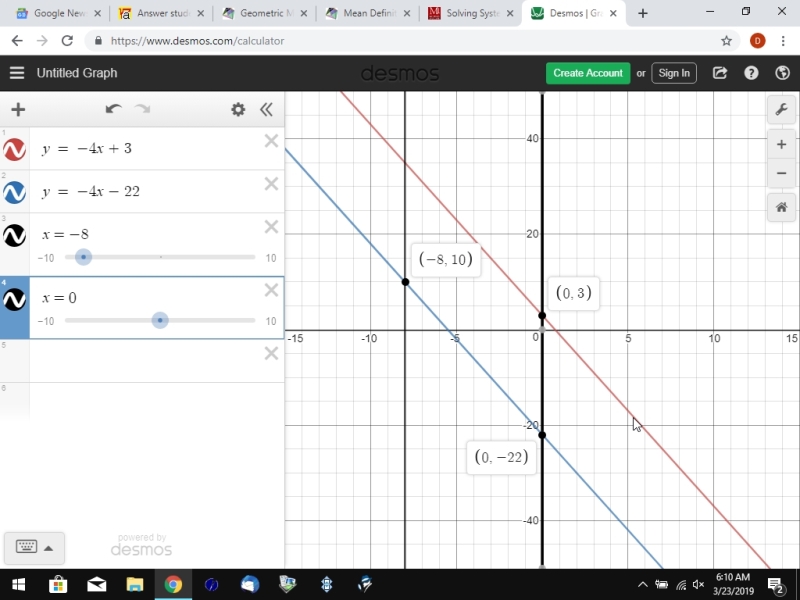
6. Passing through (-8, -10) and parallel to the line whose equation is y = -4x + 3
the slope intercept form of the equation of a straight line is y = mx = b
m is the slope and b is the y-intercept.
the equation of y = -4x + 3 has a slope of -4 and a y-intercept of 3.
your line passing through the point (-8,-10) must have a slope of -4 if it is to be parallel to the given line.
therefore, the equation of your line becomes y = -4x + b.
if your line passes through the point (-8,-10), then you can use the point slope form of the equation of a straight line to find the y-intercept.
the point slope form of the equation of a straight line is (y - y1) = m * (x - x1).
m is the slope and (x1,y1) is your point.
since your slope is -4 and your point is (-8,-10), the point slope form of the equation becomes (y + 10) = -4 * (x + 8).
simplify this equation to get y + 10 = -4 * x - 32.
subtract 10 from both sides of this equation to get y = -4 * x - 42..
your y-intercept is -42.
that's the value of y when x is equal to 0.
there is another method to find the y-intercept that works just as good.
that's to take your equation and replace y with -10 and x with -8.
y = -4x + b becomes -10 = -4 * (-8) + b
simplify to get -10 = 32 + b
subtract 32 from both sides of the equation to get -22 = b.
your y-intercept is equal to b which is equal to -22.
both methods get the same answer and you can choose which method you prefer to use.
the advantage of the second method is that is applicable to equations that are not linear as well, while the point slope form is applicable to linear equations only as far as i can tell.
i haven't seen point slope form being applied to any equations other than linear equations.
doesn't mean it's not.
it just means that i haven't seen it.
anyway, either method gets the same answer and you can choose which method you prefer.
your solution is that the equation of your line is y = -4x - 22.
that equation plus the original equation of y = -4x + 3 can be graphed as shown below.
----------------------------------------------------------------------
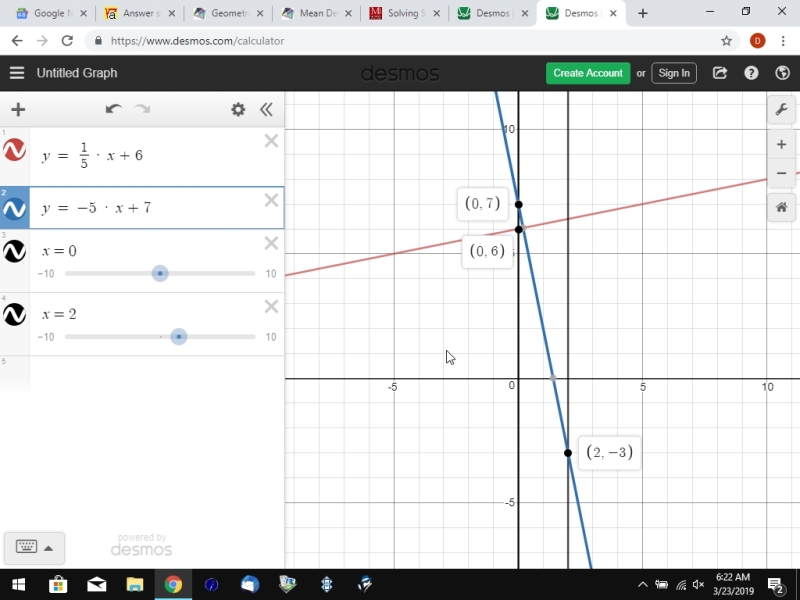
7. Passing through (2, -3) and perpendicular to the line whose equation is y = (1/5) x + 6
the slope intercept form of your line will be y = mx + b.
m is the slope
b is the y-intercept.
since your line is perpendicular to the given line, the slope must be a negative reciprocal of the slope of that line.
-5 is the negative reciprocal of 1/5.
the reciprocal is 5/1 which is equal to 5.
the negative reciprocal is -5.
the reciprocal of any number if that same number divided into 1.
the reciprocal of 1/5 is equal to 1 / (1/5) which is equal to 1 * 5/1 which is equal to 5.
the negative reciprocal is the reciprocal times -1.
anyway, the slope of your perpendicular line has to be -5.
the slope intercept form of your line is therefore y = -5 * x + b.
you need to find the y-intercept.
that was done above using two methods, so i'll skip the instructions here and tell you that the y-intercept is equal to 7.
you can use either method to confirm for your self that this is true.
the following graph will also confirm that.
----------------------------------------------------------------------
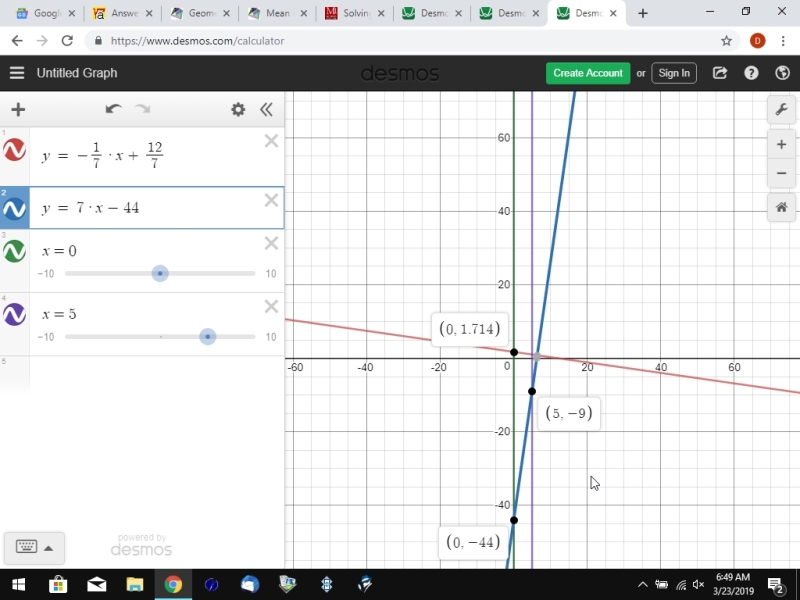
8. Passing through (5, -9) and perpendicular to the line whose equation is x + 7y - 12 = 0
if it is perpendicular, then the slope is a negative reciprocal of the slope of the given line.
the given line is not in slope intercept form.
it is in standard form.
convert it to slope intercept form as follows:
start with x + 7y - 12 = 0.
subtract x from both sides to get 7y - 12 = -x + 0.
add 12 to both sides to get 7y = -x + 12.
divide both sides by 7 to get y = -1/7 * x + 12/7.
the equation is now in slope intercept form.
the slope is -1/7.
the negative reciprocal of that is 7.
your line perpendicular to this line will have a slope of 7.
it's form is y = 7 * x + b so far.
you next need to find the y-intercept.
the line goes through the point (5,-9).
use either method described in the first problem to find the y-intercept.
the y-intercept will be -44 and the equation of the line perpendicular to the original line and passing through the point (5,-9) will be y = 7 * x - 44.
here's the graph.
here's a reference on systems of linear equations that you might find useful.
one part of that is the graphical solution.
https://www.purplemath.com/modules/systlin1.htm
----------------------------------------------------------------------
|
|
|