Question 1137151: A frustum of a regular square pyramid has bases with sides of length 6 and 10. The height of the frustum is 12, find the surface area.
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A frustum of a regular square pyramid has bases with sides of length 6 and 10. The height of the frustum is 12, find the surface area.
The areas of the two bases are easy:  and and 
To find the lateral surface area, you need to know the 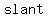 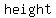 of each face. of each face.
To find that slant height, drop a perpendicular from the middle of one side of the top base to the bottom base.
With the side lengths of the two bases  and and  , that perpendicular will touch the bottom base , that perpendicular will touch the bottom base  units from the edge (half of units from the edge (half of  , minus half of , minus half of  ). ).
Then, since the height of the frustum is  , the slant height of each face, by the Pythagorean Theorem, is , the slant height of each face, by the Pythagorean Theorem, is

Each face is then a trapezoid with bases  and and  and height and height 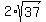 ; that makes the area of each face ; that makes the area of each face 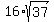 . .
So the total surface area, both bases and all four faces, is

|
|
|