Question 1136545: The pear company sells pPhones. The cost to manufacture x pPhones is C(x)=-23x^2+50000x+20461 dollars (this includes overhead costs and production costs for each pPhone). If the company sells x pPhones for the maximum price they can fetch, the revenue function will be R(x)=-26x^2+128000x dollars.
How many pPhones should the pear company produce and sell to maximize profit? (remember that profit = revenue - cost)
Not sure how to solve this question. I could use some guidance on this problem... thank you. This is written by my professor.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! as a lesson in algebra, this problem is probably ok.
as a lesson in using algebra to solve practical, real world problems, this problem is probably not ok.
reality is not necessarily your prime concern in solving this problem, so we'll concentrate on the solving of the algebra first.
you have a revenue function and you have a cost function and you want a profit function.
profit = revenue minus cost, so if you subtract the cost function from the revenue function, you will get the profit function.
your revenue function is y = -26 * x^2 + 128000 * x.
your cost function is y = -23 * x^2 + 50000 * x + 20461.
your profit function will be y = -26 * x^2 + 128000 * x - (-23 * x^2 + 50000 * x + 20461).
simplify to get y = -26 * x^2 + 128000 * x - 23 * x^2 - 50000 * x - 20461.
combine like terms to get y = -3 * x^2 + 78000 * x - 20461.
that's your profit function.
you want to know when your profit will be maximum.
since this is a quadratic function that's in standard form, you get:
a = -3
b = 78000
c = -20461.
the maximum profit will be when x = -b / 2a.
that will be when x = -78000 / -6 = 13000.
when x = 13000, y = -3 * x^2 + 78000 * x - 20461 becomes y = -3 * 13000^2 + 78000 * 13000 - 20461 which becomes y = -507,000,000 + 1,014,000,000 - 20,461 = 506,979,539
your maximum profit will be when x = 13000 and will be 506 million, 979 thousand, 539 dollars.
that solves the algebra, which, once you know how to do it, is pretty straight forward.
now to using algebra to solve a realistic problem.
this problem is not ok for the following reason.
when x = 13000, .....
revenue = -2,730,000,000
cost = -3,236,979,539
profit = revenue minus cost = 506,979,539
you get your maximum profit when revenue is negative and cost is even more negative.
this is not realistic because both revenue and cost need to be positive.
but, that's not your worry.
your worry is to find the maximum profit which we found above.
i suppose somebody could make a case for the problem being realistic, but i don't see it.
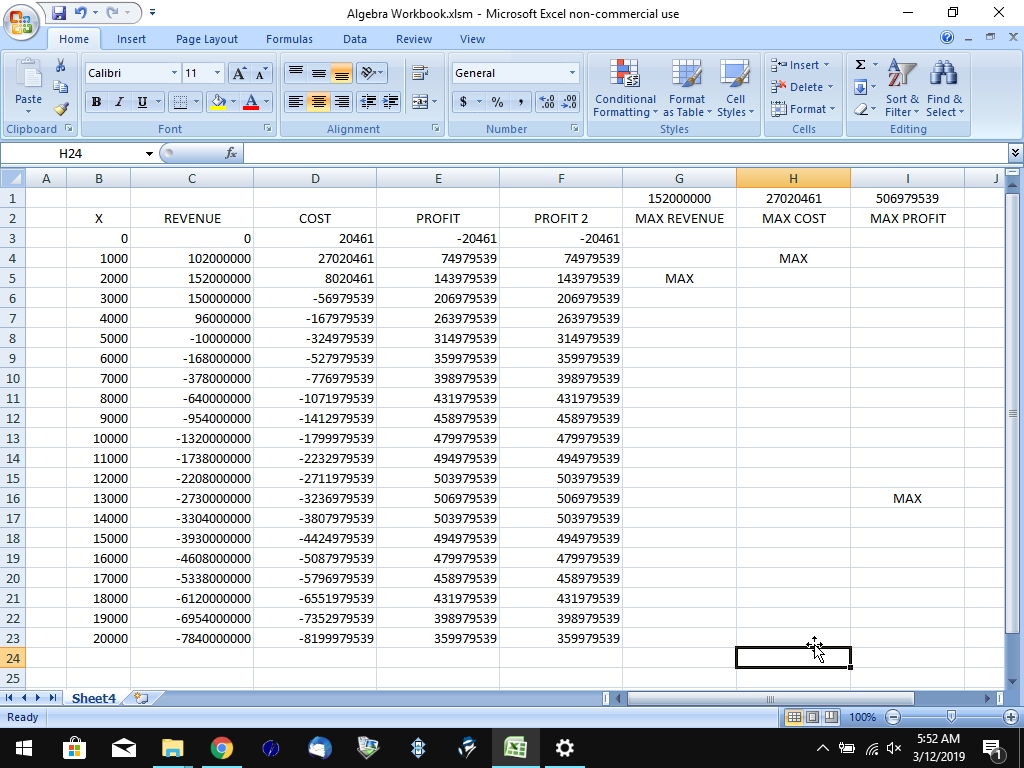
i created a spread sheet to show you the calculations for revenue, cost, and profit, for x in intervals of 1000.
it's shown below.
it also shows when the maximum revenue occurs and when the maximum cost occurs and when the maximum profit occurs.
|
|
|