Question 1125217: A bag contains three 20-dollar bills, three 10-dollar bills, and three 5-dollar bills. Three bills are selected from the bag at random. Let the random variable X represent the total dollar value of the selected bills.
What is the least possible value of X?
What is the greatest possible value of X?
What is Pr(X=30)?
Enter your answers as whole numbers or fractions in lowest terms. Your answers should all be numeric -- do not use dollar signs in your answers.
Found 2 solutions by math_helper, ikleyn:
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! A bag contains three 20-dollar bills, three 10-dollar bills, and three 5-dollar bills. Three bills are selected from the bag at random. Let the random variable X represent the total dollar value of the selected bills.
What is the least possible value of X?
This happens when all three selections are each $5 bills, 3x5 = 15:
Ans:  dollars dollars
What is the greatest possible value of X?
This happens when all three selections are $20 bills: 3x20 = 60:
Ans:  dollars dollars
What is Pr(X=30)?
Let F=five, T=ten, W=twenty selected
Lets list the probabilities where a ten is selected first, then any of {F,T,W} for the remaining two:
Pr(TTT) = (3/9)(2/8)(1/7) = 6/504
Pr(TTF) = (3/9)(2/8)(3/7) = 18/504
Pr(TTW) = (3/9)(2/8)(3/7) = 18/504
Pr(TWW) = 18/504
Pr(TFF) = 18/504
Pr(TWF) = 27/504
Pr(TFW) = 27/504
Pr(TFT) = 18/504
Pr(TWT) = 18/504
Similarly for Pr(F,*,*) and Pr(W,*,*) (not shown, but they follow the same pattern, for instance if you want Pr(F,W,F) just look above for Pr(T,W,T), mentally substituting "F" for "T" and you can see it is 18/504)
Pr(X=30) = Pr(three tens) + Pr(two fives and one twenty)
Pr(X=30) = Pr(T,T,T) + Pr(F,F,W) + Pr(F,W,F) + Pr(W,F,F)
= 6/504 + 18/504 + 18/504 + 18/504
= 60/504
=  (about 0.1190 or 11.9%) (about 0.1190 or 11.9%)
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The solution by the tutor @math-helper is fine.
I want to show you different way to solve the last part.
There are two ways to get 30: 30 = 10+10+10 and/or 30 = 20 + 5 + 5.
There are no other ways.
In all, there are 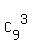 = =  = 84 different groups of three banknotes (without looking the order).
Of these 84 groups, there is only one group containing 3 "tens". It contributes = 84 different groups of three banknotes (without looking the order).
Of these 84 groups, there is only one group containing 3 "tens". It contributes 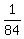 to the total probability.
Also, there are 9 groups containing (20,5,5) in any order.
(9 = 3 ways to get 20 from the 3 "T" MULTIPLIED by 3 ways to get the pair (5,5) from 3 "F").
It contributes to the total probability.
Also, there are 9 groups containing (20,5,5) in any order.
(9 = 3 ways to get 20 from the 3 "T" MULTIPLIED by 3 ways to get the pair (5,5) from 3 "F").
It contributes 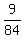 to the total probability.
So, the total probability under the question for this part of the problem is to the total probability.
So, the total probability under the question for this part of the problem is 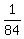 + + 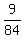 = = 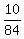 = = 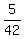 ,
which coincides with the answer by the tutor @math-helper. ,
which coincides with the answer by the tutor @math-helper.
------------------
On Combinations, see the lessons
- Introduction to Combinations
- PROOF of the formula on the number of Combinations
- Problems on Combinations
- OVERVIEW of lessons on Permutations and Combinations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|