Question 1124738: Xiao Li wishes to accumulate $50,000 by the end of 10 years by making equal annual end-of-year deposits over the next 10 years. If Xiao Li can earn 5 percent on her investments, how much must she deposit at the end of each year?
Answer by ikleyn(52946)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It is a classic Ordinary Annuity saving plan. The general formula is
FV =  ,
where FV is the future value of the account; P is annual payment (deposit); r is the annual percentage yield presented as a decimal;
n is the number of deposits (= the number of years, in this case).
From this formula, you get for for the annual payment
P = ,
where FV is the future value of the account; P is annual payment (deposit); r is the annual percentage yield presented as a decimal;
n is the number of deposits (= the number of years, in this case).
From this formula, you get for for the annual payment
P =  . (1)
Under the given conditions, FV = $50,000; r = 0.05; n = 10. So, according to the formula (1), you get for the annual payment
P = . (1)
Under the given conditions, FV = $50,000; r = 0.05; n = 10. So, according to the formula (1), you get for the annual payment
P = 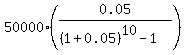 = $3975.23.
Answer. The necessary annual deposit value is $3975.23.
Note that of projected $50,000 the total of Xiao Li's deposits will be only 10 times $3975.23, i.e. 39,752.30 dollars.
The rest is what the account will earn/accumulate/accrue in 10 years. = $3975.23.
Answer. The necessary annual deposit value is $3975.23.
Note that of projected $50,000 the total of Xiao Li's deposits will be only 10 times $3975.23, i.e. 39,752.30 dollars.
The rest is what the account will earn/accumulate/accrue in 10 years.
---------
On Ordinary Annuity saving plans, see the lessons
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
in this site.
|
|
|