Question 1124097: J, K, and L are events in sample space S.
Pr(J)=0.35
Pr(K)=0.18
Pr(L)=0.24
Pr(J∩K)=0.11
Pr(J′∩L′)=0.55
Pr(K′∩L)=0.16
What is Pr(J|K)?
What is Pr(L|J)?
What is Pr(K|L′)?
Enter your answers as whole numbers or fractions in lowest terms.
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20055)   (Show Source):
You can put this solution on YOUR website! J, K, and L are events in sample space S.
Let's draw the Venn diagram with 3 sets where
the large rectangle represents the sample space S.
The letters "a" through "h" will represent the
probabilities of the regions in which the letters
are located:
S
Pr(J) = a+b+d+e = 0.35
Pr(K) = b+c+e+f = 0.18
Pr(L) = d+e+f+g = 0.24
Pr(J∩K) = b+e = 0.11
Pr(J′∩L′) = c+h = 0.55
Pr(K′∩L) = d+g = 0.16
Also since S is the sample space:
Pr(S) = a+b+c+d+e+f+g+h = 1
We have this system of equations
a+b+c+d+e+f+g+h = 1.00
a+b +d+e = 0.35
b+c +e+f = 0.18
d+e+f+g = 0.24
b +e = 0.11
c +h = 0.55
d +g = 0.16
By matrix methods using a TI-83 or TI-84,
we can solve for "a" through "g" in terms of "h"
a = 0.66-h
b = h-0.45
c = 0.55-h
d = h-0.42
e = 0.56-h
f = h-0.48
g = 0.58-h
What is Pr(J|K)?
Pr(J|K) = Pr(J∩K)/Pr(K) = (b+e)/(b+c+e+f) =
[(h-0.45)+(0.56-h)]/[(h-0.45)+(0.55-h)+(0.56-h)+(h-0.48)] =
(h-0.45+0.56-h)/(h-0.45+0.55-h+0.56-h+h-0.48) =
(-0.45+0.56)/(-0.45+0.55+0.56-0.48) =
0.11/0.18 = 11/18
-------------------
What is Pr(L|J)?
Pr(L|J) = Pr(L∩J)/Pr(J) = (d+e)/(a+b+d+e) =
[(h-0.42)+(0.56-h)]/[(0.66-h)+(h-0.45)+(h-0.42)+(0.56-h)] =
(h-0.42+0.56-h)/(0.66-h+h-0.45+h-0.42+0.56-h) =
(-0.42+0.56)/(0.66-0.45-0.42+0.56) =
0.14/0.35 = 14/35 = 2/5
-------------------
What is Pr(K|L')?
Pr(K|L') = Pr(K∩L')/Pr(L') = (b+c)/(a+b+c+h) =
[(h-0.45)+(0.55-h)]/[(0.66-h)+(h-0.45)+(0.55-h)+h] =
(h-0.45+0.55-h)/(0.66-h+h-0.45+0.55-h+h) =
(-0.42+0.56)/(0.66-0.45-0.42+0.56) =
(-0.45+0.55)/(0.66-0.45+0.55)
0.10/0.76 = 10/76 = 5/38
Edwin
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
J, K, and L are events in sample space S.
Pr(J)=0.35
Pr(K)=0.18
Pr(L)=0.24
Pr(J∩K)=0.11
Pr(J′∩L′)=0.55 (*)
Pr(K′∩L)=0.16 (**)
What is Pr(J|K)?
What is Pr(L|J)?
What is Pr(K|L′)? ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Although the answer produced by Edwin is correct, I do not think
that his approach and his solution are adequate and that they are how they expected to be.
I put here my solution, and after completing it, I put my reasons why I think the Edwin' solution and approach are inadequate.
1. What is Pr(J|K) ?
Pr(J|K) = by the definition = Pr(J∩K)/Pr(K) =  =  .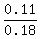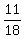
2. What is Pr(L|J) ?
In the "given" part, find a line (*) related to L and J.
This line is Pr(J' ∩ L')=0.55
From the elementary set theory, J' ∩ L' = (S\J) ∩ (S\L) = S \ (J U L). (Symbol " \" means subtraction of sets.)
You can prove it on your own using (or without using) Venn diagram for 2 subsets J and L in S.
Also, from the basics of probability, Pr(J U L) = Pr(J) + Pr(L) - Pr((J ∩ L).
These pieces are THE KEY part of the solution, which you SHOULD and MUST understand when solving such problems !
Therefore, 0.55 = Pr(J' ∩ L') = 1 - (Pr(J) + Pr(L)) + Pr((J ∩ L).
which implies Pr(J ∩ L) = 0.55 + Pr(J) + Pr(L) - 1 = 0.55 + 0.35 + 0.24 - 1 = 0.14.
Therefore,
Pr(L|J) = by the definition = Pr(L∩J)/Pr(K) =  =  .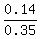
3. What is Pr(K|L')?
By the definition, Pr(K|L') = P(K ∩ L')/P(L').
Pr(L') = 1 - Pr(L) = 1 - 0.24 = 0.76.
What is P(K ∩ L') ?
In the "given" part, find a line (**) related to K and L.
This line is Pr(K' ∩ L)=0.16.
The set (K' ∩ L) is "L without K", or, in other words, L\ (L ∩ K).
Hence, Pr((K' ∩ L) = 0.16 = Pr(L) - Pr(L ∩ K), which gives
Pr(L ∩ K) = Pr(L) - 0.16 = 0.024 - 0.16 = 0.08.
The set (K ∩ L') is "K without L", or, in other words, K\ (L ∩ K).
Hence, Pr(K ∩ L') = 0.18 - Pr(L ∩ K) = 0.18 - 0.08 = 0.10.
Thus finally Pr(K|L') =  =  .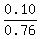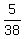
So my answers coincide with that by Edwin. Which is good.
This problem is not of the school Math level. It is of the level of introductory problems to a Probability theory course
at an advanced Math college or a renowned University.
And the goal of such exercises is to teach the students to basic operations on the sets and to connect it with the basics of Probability.
It is an approach I followed in my solution.
Every of the three questions of this assignment should be answered based o information related to relevant two sets of each question.
There is no any need to involve the third set.
There is no any need to use Venn diagram for three sets.
There is no any need to construct the system of 7 equations and solve it.
It is why I chose another, more adequate approach and wrote this post.
---------------------
I am not seeking for a war with Edwin.
In opposite, I esteem him as a great tutor at this forum, and, probably, had I not see his post, I would not write this one.
|
|
|
