Question 1119204: I kind of get that when you are solving an inequality like ∣5x+1∣>3 that you are supposed to do it in two cases. But, what I don't get is why one of those cases is 5x+1<−3 because I thought that absolute values can never be negative. Why do we do that case?
Found 3 solutions by addingup, ikleyn, MathTherapy:
Answer by addingup(3677)   (Show Source):
You can put this solution on YOUR website! An absolute number cannot be negative. Pretend you are at the zero line and take two steps left, now you are standing on -2. Next I ask you to go back to the zero line and take two steps right. Now you're standing on the +2. But both times you took two steps. Absolute value doesn't care about the direction, only about the distance.
To solve your equation:
∣5x+1∣>3 to solve, we rewrite:
5x+1>3 subtract 1 on both sides
5x > 2 divide both sides by 5
x > 2/5 so your yardstick is 2/5 to the right, in the positive. And how far does it go to the left, to the negative? Because the answer will let you calculate the length of your yardstick
5x+1>-3
5x>-4
x<-4/5 (notice the change in the direction of the sign because, from zero, we are decreasing 4/5)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
So, how long is your yardstick? It goes from -4/5 on the left to 2/5 on the right:
2/5--4/5 = 6/5 = 1.2 This is how long your yardstick is.
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
1. If you are given inequality |a| > 3 for real number "a", it means that
EITHER a > 3 OR a < -3.
It is VERY FIRST thing you need to understand.
The rest is just technique, which I'll show you below.
To get this understanding, use the visual image of the number line and remember that |a| > 3 means that the distance from "a" to 0
(to zero) is greater than 3.
2. After you got this understanding, the rest is MUCH EASIER.
So, |5x+1| > 3 means that
EITHER 5x+1 > 3 OR 5x+1 < -3.
3. Let us consider the case
5x+1 > 3 (1)
first. Subtract 1 from both sides. You will get
5x > 3 - 1 = 2. Divide by 5 both sides. You will get
x >  , or x > 0.4.
It is your solution for the case (1).
4. Next consider the case
5x + 1 < -3.
Subtract 1 from both sides. You will get
5x < -3 -1 = -4.
Divide by 5 both sides. You will get
x < 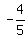 or x < -0.8.
It is your solution for the case (2).
5. Thus the set of solutions to the given inequality is the UNION of two semi-infinite intervals
{ x < -4/5 } U { x > 2/5 }.
Solved.
If after my explanations you still have questions, do not hesitate post them to the forum.
===============
I wrote my solution, because the solution by the other tutor contained some errors on the way, that could confuse you.
So, I rectified his solution and his answer as well.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! I kind of get that when you are solving an inequality like ∣5x+1∣>3 that you are supposed to do it in two cases. But, what I don't get is why one of those cases is 5x+1<−3 because I thought that absolute values can never be negative. Why do we do that case?
You're correct in that absolute values can never be negative (< 0).
However, when you do the "case" 5x + 1 < - 3, you have omitted the absolute-value bars, so you now have a regular inequality to solve.
|
|
|
