Question 1116225: HOW do I do this?:
Solve each absolute value inequality and show it's solution set:
a)|x|≤3
b)|3−x|<5
c)|4g−5|>17
d)|4x+1|<21
Found 3 solutions by stanbon, greenestamps, ikleyn:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! HOW do I do this?:
Solve each absolute value inequality and show it's solution set:
a)|x|≤3
-3<= x <=3
====================
b)|3−x|<5
-5 < 3-x < 5
-9 < -x > 2
-2 < x < 9
====================
c)|4g−5|>17
4g-5 < -17 or 4g-5 > 17
g < -3 or g > 11/2
------------------------------
d)|4x+1|<21
-21 < 4x+1 < 21
-22 < 4x < 20
-11/2 < x < 5
------------------
Cheers,
Stan H.
------------------
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(1) The inequality

where b is a non-negative number, means the value of x-a is between -b and b:

As an example, suppose the inequality is

We can find the solution set using the pattern shown above:


The solution set in interval notation is [-4,10]
(2) Here is another way of interpreting the same inequality
This interpretation is helpful when the inequalities get more complicated.
The inequality

means the difference between x and a is less than or equal to b. On a number line, that means x can be any number whose distance from a is at most b.
So the same example as above,

has as its solution set all the numbers whose distance from 3 is at most 7.
This is easy to see on a number line; 7 to the left of 3 is -4, and 7 to the right is 10, so the solution set is all values of x from -4 to 10.
Note that for the inequality 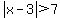 the solution set is all values of x that are OUTSIDE the interval from -4 to 10. So the solution set for that inequality would be (-infinity, -4) union (10,infinity). the solution set is all values of x that are OUTSIDE the interval from -4 to 10. So the solution set for that inequality would be (-infinity, -4) union (10,infinity).
Solving that kind of inequality with the first method requires solving two equations separately; with the second method you simply have a solution set that is all the values that are NOT between -4 and 10 on the number line.
You can use either of these interpretations to solve each of your examples. If you really want to learn about solving inequalities, you should solve each of your examples by BOTH methods.
Here are some hints for helping you with your examples:
(a) 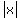 is the same as is the same as 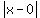
(b) 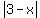 is the same as is the same as 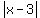
(c) You can divide both sides of an inequality by a positive constant. So 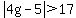 is equivalent to is equivalent to 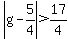 . Note also in this problem the solution set is the set of values for which the absolute value of the expression is GREATER THAN some number. So the solution set will be the set of all numbers OUTSIDE of some interval -- that is, it will be the union of two intervals. . Note also in this problem the solution set is the set of values for which the absolute value of the expression is GREATER THAN some number. So the solution set will be the set of all numbers OUTSIDE of some interval -- that is, it will be the union of two intervals.
(d) Again divide both sides by 4 to get 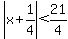
Answer by ikleyn(52785)   (Show Source): (Show Source):
|
|
|