Question 1114951: Find the equation of the straight line perpedicular to line y =x^ 2+ 1,and passing through the point (4,5).
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The solution by @josgarithmetic is incorrect.
Below please find the correct solution.
First, the given point (4,5) does not belong to the parabola y = x^2 + 1.
Everybody can check it in 3 seconds.
Therefore, it is INCORRECT to evaluate the slope of 2x at this point.
This slope must be evaluated at the point ON THE CURVE, instead.
So, my solution starts stating that 2x is the slope of the tangent line at the (unknown) point on the parabola y = x^2+1.
Therefore, the slope of the perpendicular line to the curve is  .
Now I can write the equation for the perpendicular line having the slope of .
Now I can write the equation for the perpendicular line having the slope of  and passing through the points (x,y) and (4,5),
where x is unknown and y = x^2+1: and passing through the points (x,y) and (4,5),
where x is unknown and y = x^2+1:
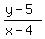 = =  , ,
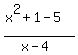 = =  , ,
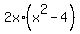 = -x+4 = -x+4
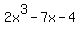 = 0.
The plot of the last polynomial is shown in the Figure 1 below. = 0.
The plot of the last polynomial is shown in the Figure 1 below.
 Figure 1. Plot y =
Figure 1. Plot y = 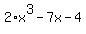 The polynomial has 3 roots, and the roots are irrational numbers (they are not rational).
I used Excel "What-if-Analysis" and calculated these roots approximately, with 3 decimals after the decimal point.
The roots are x= 2.109, -0.650 and -1.46, giving the values for the slopes m =
The polynomial has 3 roots, and the roots are irrational numbers (they are not rational).
I used Excel "What-if-Analysis" and calculated these roots approximately, with 3 decimals after the decimal point.
The roots are x= 2.109, -0.650 and -1.46, giving the values for the slopes m =  m = -0.237, 0.769 and 0.343 respectively.
So, the three lines satisfying the condition of perpendicularity are
y = -0.237*(x-4)+5, y = 0.769*(x-4)+5, and y = 0.343*(x-4)+5.
These lines, together with the parabola y = x^2+1, are shown in the Figure 2 below.
m = -0.237, 0.769 and 0.343 respectively.
So, the three lines satisfying the condition of perpendicularity are
y = -0.237*(x-4)+5, y = 0.769*(x-4)+5, and y = 0.343*(x-4)+5.
These lines, together with the parabola y = x^2+1, are shown in the Figure 2 below.
 Figure 2. Plot y =
Figure 2. Plot y = 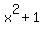 (red), y = -0.237*(x-4)+5 (green), y = 0.769*(x-4)+5 (blue), y = 0.343*(x-4)+5 (purple)
Notice that the intersection of these straight lines is exactly the given point (4,5). (red), y = -0.237*(x-4)+5 (green), y = 0.769*(x-4)+5 (blue), y = 0.343*(x-4)+5 (purple)
Notice that the intersection of these straight lines is exactly the given point (4,5).
Solved.
|
|
|