Question 1112713: A test is available to diagnose a disease. If a person has the disease, the probability that the test will produce a positive signal is 0.98. If a person does not have the disease, the probability that the test will produce a positive signal is 0.02. Assume that the proportion of people in the community who have the disease is 0.05
Given that the test is negative, what is the probability that the person does not have the disease?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Out of 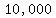 people, people,  have the disease. have the disease.
Of those,  test positive, and start looking for treatment. test positive, and start looking for treatment.
The other  test negative, test negative,
and do not think they have the disease, but they do.
Out of the same 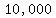 people, another people, another  people do not have the disease. people do not have the disease.
However, among them,  test positive, and worry unnecessarily. test positive, and worry unnecessarily.
The remaining  people without the disease test negative. people without the disease test negative.
Out of the whole 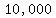 people, people,
there are  people who have tested negative. people who have tested negative.
Out of those who tested negative, the fraction without the disease is
  . .
That is the probability that a person who tests negative does not have the disease.
|
|
|