Question 1112436: Silas is about to begin regular month-end contributions of $500 to a bond fund. The fund's long-term rate of return is expected to be 6% compounded semiannually. Rounded to the next higher month, how long will it take Silas to accumulate $300,000?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! he is making monthly contributions of 500 to a bond fund.
the fund's long term rate of return is expected to be 6% compounded semi-annually.
how long will it take Silas to accumulate $300,000?
6% per year is the nominal interest rate.
6% compounded semi-annually is equal to 6% / 2 = 3% every semi-annual period.
1.03^2 = 1.0609, which is the effective annual interest rate.
1.0609 ^ (1/12) = 1.004938622.
subtract 1 from that and you have the effective monthly interest rate.
you are making contributions of 500 at the end of each month.
the future value is expected to be 300,000.
you can solve this in the following manner, using the TI-BA-II calculator.
enter PV = 0
enter PMT = -500
enter FV = 300,000
enter I/Y = 1.004938622 - 1 = .004938622 * 100 = .4938622%.
compute N to get N = 279.5197879 months.
when you do it the way i showed you above, you have to make sure that the calculator is set as follows:
P/Y = 1
C/Y = 1
i won't tell you how to do it because you may not even have the TI-BA-II calculator, and, if you do, you're better off reading the instructions for that calculator.
there is another way to do it using the TI-BA-II calculator that's a good way to check if you did it right.
you set P/Y = 12 and C/Y = 2
that's 12 payments per year and 2 compounding periods per year.
when you do that, you set the following"
PV = 0
PMT = -500
FV = 300,000
I/Y = 6%
then compute for N.
you should get N = 279.5197879 months.
that's the same answer as we got before.
this tells you that you did it right, even if you might not understand completely what's going on.
i did it both ways and i got the same answer, so i assume the answer is correct, because the TI-BA-II is programmed to handle this type of problem and i got the same answer when i did it manually through formula manipulation.
i also used excel as a reasonable check.
i got the balance is equal to 300,000 some time between the 279th month and the 280th month.
that's close enough to indicate that the TI-BA-II did it correctly.
the difficulty in showing what's really happening is that the interest is accruing every month, but is not compounded until every 6th month.
until i'm able to show what's actually going on, i'm going on faith that the TI-BA-II is doing it correctly and, if i can duplicate the answer that the TI-BA-II tells me when P/Y = 12 and C/Y = 3, then i must be doing it correctly as well.
bottom line is:
TI-BA-II is programmed to tell you directly when P/Y = 12 and C/Y = 3.
you can also used excel to confirm your answer is reasonable.
my confirmation is shown below:
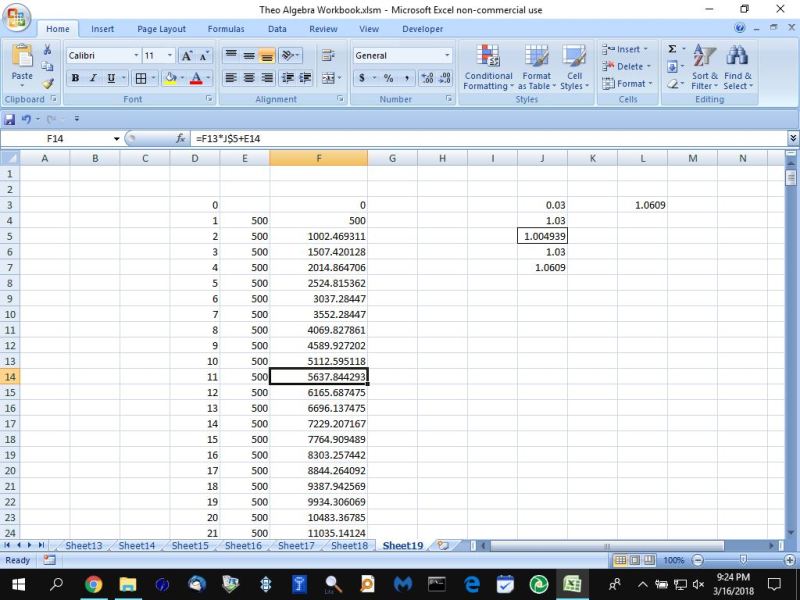
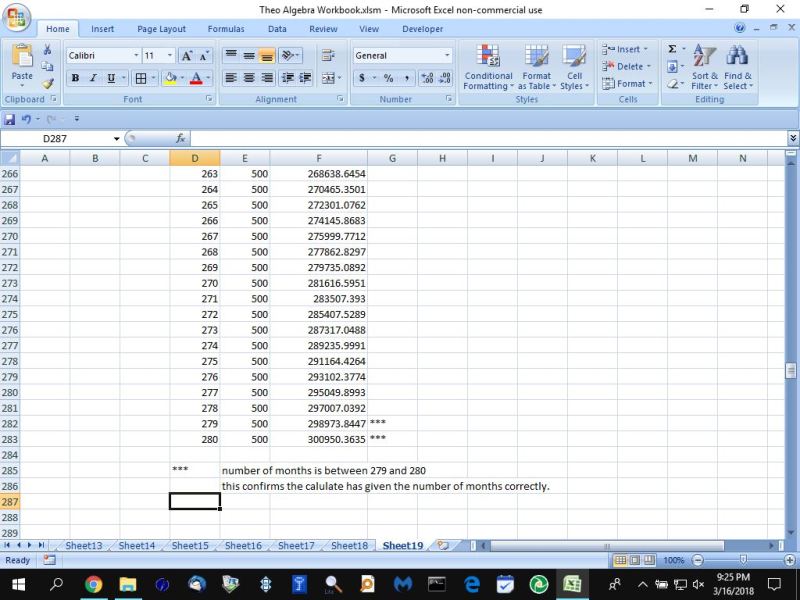
months 22 to 262 are not shown.
you can see that, somewhere between the 279th month and the 280th month, the balance becomes 300,000.
you can also do this with manual formulas, but i won't get into that now.
the trick, however, is to get the effective interest rate per year and then find the effective interest per month from that.
in summary, what i did is the following.
annual interest rate is 6%.
semi-annual interest rate is 6% / 2 = 3%.
effective annual interest rate is 1.03^2 = 1.0609 - 1 = .0609 * 100 = 6.09%.
effective monthly interest rate is 1.03 ^ (1/6) = 1.004938622 - 1 = .004938622 * 100 = .4938622%.
you can see that the effective monthly interest rate will get you the effective annual interest rate by taking 1.004938622 and raising it to the 12th power to get 1.0609
if you use manual formulas, you would use a monthly interest rate of .004938622.
the financial calculators use percent.
the manual formulas use rate, which is percent / 100.
one of these days i'll be able to figure out how to show what's really going on, but so far i haven't been able to do so.
until then, i'm trusting that the TI-BA-II calculator does it the right way when you use P/Y = 12 and C/Y = 2.
|
|
|