Question 1112384: You are the marketing director for a company that manufactures bodybuilding supplements and you are planning to run ads in Sports Illustrated and GQ Magazine. Based on readership data, you estimate that each one-page ad in Sports Illustrated will be read by 640,000 people in your target group, while each one-page ad in GQ will be read by 160,000. You would like your ads to be read by at least 3 million people in the target group and, to ensure the broadest possible audience, you would like to place at least three full-page ads in each magazine. Draw the feasible region that shows how many pages you can purchase in each magazine. (Let x be the number of full-page ads in Sports Illustrated and let y be the number of full-page ads in GQ Magazine.) Find the corner points of the region.
(x, y) = (smaller x-value)
(x, y) = (larger x-value)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! x = number of full page ads in Sports Illustrated.
y = number of full page ads in GQ.
you want to put at least 3 full page ads in Sports Illustrated and at least 3 full page ads in GQ.
the formula for that is:
x >= 3 and y >= 3
each full page ad in Sports Illustrated is estimated to be read by 640,000 readers in the target group.
each full page ad in GQ is estimated to be read by 160,000 readers in the target group.
you want to reach at least 3 million readers.
the formula for that is:
640,000 * x + 160,000 * y >= 3,000,000
those are your constraint inequalities.
x >= 3
y >= 3
640,000 * x + 160,000 * y >= 3,000,000
using the desmos.com calculator, you would graph the opposite of these inequalities.
in other words, you would graph:
x <= 3
y <= 3
640,000 * x + 160,000 * y <= 3,000,000
the region of the graph that is NOT shaded is your region of feasibility.
here's what the graph looks like.
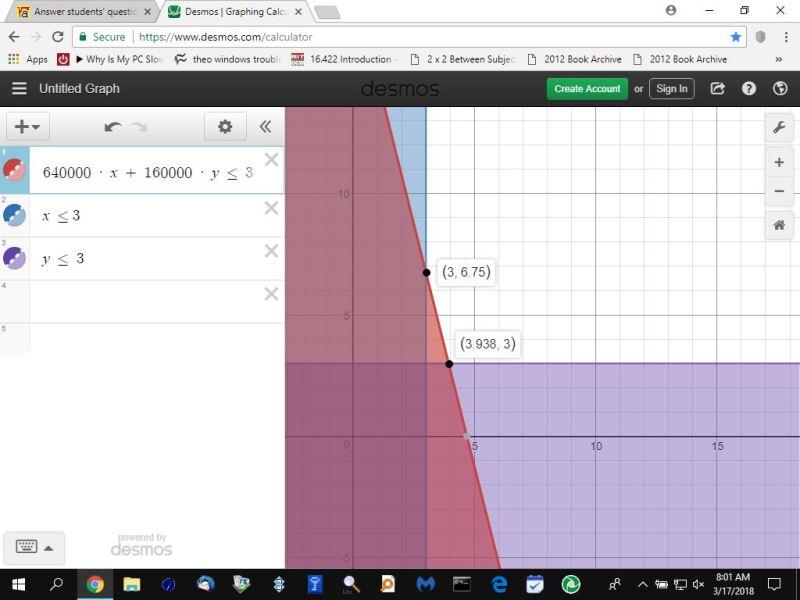
the smaller x value is 3.
it is paired with the y value of 6.75.
this means 3 full page ads in Sports Illustrated and 6.75 full page ads in GQ.
you would probably round up to the next highest integer.
3 * 640,000 + 6.75 * 160,000 = 3,000,000
3 * 640,000 + 7 * 160,000 = 3,040,000.
the constraints are satisfied.
x >= 3 and y >= 3
640,000 * x + 160,000 * y >= 3,000,000
the larger x-value is 3.938.
it is paired with the y-value of 3.
that means 3.938 full page ads in Sports Illustrated and 3 full page ads in GQ.
once again, you would probably round up to the next highest integer.
3.938 * 640,000 + 3 * 160,000 = 3,000,320
4 * 640,000 + 3 * 160,000 = 3,040,000
the constraints are satisfied.
x >= 3 and y >= 3
640,000 * x + 160,000 * y >= 3,000,000.
your solution is that the corner points of the region are:
(x,y) = (3,6.75) for the smaller value of x.
(x,y) = (3.938,3) for the larger value of x.
|
|
|