Question 1110580: Planet A's satellite has an elliptical orbit described by
X`2/(4963)`2+ Y`2/4796`2=1
(All units are in miles.) The coordinates of the center of Planet A are(21,0). Complete parts a and b below.
. The perigee of the satellite's orbit is the point that is nearest Planet A's center. If the radius of Planet A is approximately 4063 miles, find the distance of the perigee above Planet A's surface.
The perigee's distance above Planet A's surface is
879 miles.
b. The apogee of the satellite's orbit is the point that is the greatest distance from Planet A's center. Find the distance of the apogee above Planet A's surface.
The apogee's distance above Planet A's surface is __________miles.
Found 2 solutions by KMST, ikleyn:
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! As we do not know the radius or diameter of the satellite,
we are left to assume that its position and distances to the planet's surface are measured to the center of the satellite.
All distances are in miles, so the length unit is omitted from the calculations.
If the coordinates of the center of the satellite,  ,
satisfy equation  , with  ,
the orbit would look like this:
 , with  .
If the planet center is at a point  with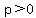 
 would be the pericenter or periapsis,
and  would be the apocenter or apoapsis.
Those are the points where the satellite is closest and farthest from the planet, respectively.
(If the planet were Earth, those points would be called perigee and apogee).
A sketch showing those points and the planet on the coordinate plane
(drawn not to scale for clarity) is shown below:
with  and  .
If the radius of the planet is  ,
knowing from the sketch that  ,
when the satellite is closest to the planet, at ,
we calculate its distance to the planet surface as
 .
That distance is  .
When the satellite is farthest to the planet, at ,
its distance from the planet surface is
 .
That distance is  .
NOTE:
As the problem provides to data that would be unnecessary
for anyone familiar with orbits and ellipses,
and calculations show the data to be contradictory,
the solution above assumes no knowledge of focal distance of an ellipse, or physics.
Otherwise, the problem makes no sense to me,
and I believe it would feel just as wrong to anyone who has studied physics, pre-calculus/calculus, and/or astrophysics,
but feel free to get second and further opinions.
I assume that it is a problem for students who have not studied ellipses or physics,
and any knowledge of physics or ellipses should be ignored when solving the problem.
The equation given would make the semi-major axis and semi-minor axis
 and  respectively.
In turn, those values would make the focal distance of the ellipse
(with as many decimal places as my calculator and computer will give me).
Physics say that should be equal to the distance between 
and the center of the planet,  .
That should be  if the center of the planet is at  .
Answer by ikleyn(52781)  (Show Source):
|
|
|
