Question 1109373: A rectangular field is 80 meters long and N meters wide. A scale drawing of the field is N centimeter long and 5 centimeter wide . Find N
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The length:width ratio is
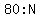 or or 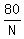 for the field measurements, for the field measurements,
and 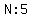 or or  for the scale drawing. for the scale drawing.
Because it is a scale drawing, those ratios are the same, so
 . .
Solving that equation, we get


 . .
So, the field is 20 meters wide,
and the scale drawing is 20 centimeters long.
NOTES:
1) The length:width ratios are numbers with no units:
 and and  . .
Unless you convert units, the scale factor is a ratio with units:
  or or
 . .
2) The problem could have been solved by equating
"calculated" scale factors for length and width,
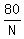 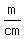 or or 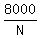 for length, for length,
and  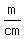 or or 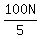 for width. for width.
That is a different reasoning,
and may be a teacher-preferred way to the solution,
but both reasoning are sound and lead to the same result.
In this case, equations without explanations may not raise teacher's objections.
Using the scale factors with 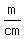 units, units,
equating scale factors leads to the same
 equation listed above, equation listed above,
because the same  was given for width of one rectangle was given for width of one rectangle
and length of the other one.
|
|
|