Question 1108845: Let n be a three digit number and let m be the number obtained by reversing the order of the digits in n. Suppose that m does not equal n and that n+m and n-m are both divisible by 7. Find all such pairs n and m.
I have found
168 and 861
259 and 952
Are there any more?
Found 2 solutions by ankor@dixie-net.com, KMST:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! No, I wrote a short basic program when you submitted it before and it spit out the two pairs that you have there. I did not submit a solution because I could not come up with logical way to find them on paper. All I could find is the difference in the reversed number. Reversed 3 digit numbers, as you no doubt know, are multiples of 99, the difference here will be 7*99 = 693. That is far as I got with it. Not much help just information. ankor@att.net
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are no other solutions. My proof is below.
The kids at artofproblemsolving would read it and laugh.
They would probably say that it was obvious based on the Ruszcyk theorem,
or some such thing.
(I just made that theorem up, but they probably have a few modular arithmetic theorems).
Let the numbers be made of the digits  , ,  , and , and  . .
 and and  are 3-digit numbers, so are 3-digit numbers, so 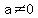 and and 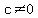 . .
To have 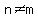 , it must be , it must be  , ,
and to have 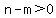 , it must be , it must be 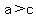 . .
For any two numbers x and y,
if x-y and x+7 are both multiples of 7,
x and y are both multiples of 7,
and vice versa.
So, m and n must be multiples of 7.
For  to be a multiple of 7, to be a multiple of 7,
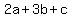 must be a multiple of 7. must be a multiple of 7.
Similarly, for  to be a multiple of 7, to be a multiple of 7,
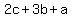 must be a multiple of 7. must be a multiple of 7.
If 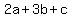 and and 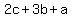 are both multiples of 7, are both multiples of 7,
 must be a multiple of 7, and must be a multiple of 7, and
 must be a multiple of 7, must be a multiple of 7,
which means 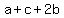 must be a multiple of 7. must be a multiple of 7.
For 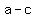 to be a multiple of 7, the only choices are to be a multiple of 7, the only choices are
 and and  . .
With  , ,  , ,
and then for  to be a multiple of 7, to be a multiple of 7,
it must be  , ,  . .
So one solution is  or or  . .
With  , ,  , ,
and then for  to be a multiple of 7, to be a multiple of 7,
it must be  , ,  . .
So the other solution is  or or  . .
|
|
|